
設函數![]() ,其中
,其中![]() 。
。
(I)解不等式![]() ;
;
(II)證明:當![]()
![]() 時,函數
時,函數![]() 在區(qū)間
在區(qū)間![]() 上是單調函數。
上是單調函數。
本小題主要考查不等式的解法、函數的單調性等基本知識,分類討論的數學思想方法和運算、推理能力.
(Ⅰ)解:不等式f(x)≤1即![]() ≤1+ax,
≤1+ax,
由此得1≤1+ax,即ax≥0,其中常數a>0,
所以,原不等式等價于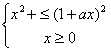 ,
,
即 ![]()
所以,當0<a<1時,所給不等式的解集為{x|0≤x≤![]() };
};
當a≥1時,所給不等式的解集為{x|x≥0}.
(Ⅱ)證明:在區(qū)間[0,+∞)上任取x1,x2使得 x1<x2.
f(x1)-f(x2)=![]() -
-![]() -a(x1-x2)
-a(x1-x2)
=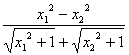 -a(x1-x2)
-a(x1-x2)
=(x1-x2)(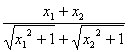 -a).
-a).
∵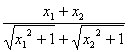 <1,且a≥1,
<1,且a≥1,
∴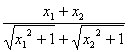 -a<0.
-a<0.
又 x1-x2<0,
∴f(x1)-f(x2)>0,
即 f(x1)>f(x2).
所以,當a≥1時,函數f(x)在區(qū)間[0,+∞)上是單調遞減函數.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案科目:高中數學 來源:2013-2014學年湖南汝城第一中學、長沙實驗中學高三11月聯考理數學卷(解析版) 題型:解答題
設函數 ,其中
,其中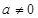 .
.
(I)若函數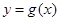 圖象恒過定點P,且點P關于直線
圖象恒過定點P,且點P關于直線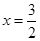 的對稱點在
的對稱點在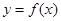 的圖象上,求m的值;
的圖象上,求m的值;
(Ⅱ)當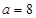 時,設
時,設 ,討論
,討論 的單調性;
的單調性;
(Ⅲ)在(I)的條件下,設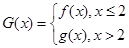 ,曲線
,曲線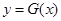 上是否存在兩點P、Q,使△OPQ(O為原點)是以O為直角頂點的直角三角形,且斜邊的中點在y軸上?如果存在,求a的取值范圍;如果不存在,說明理由.
上是否存在兩點P、Q,使△OPQ(O為原點)是以O為直角頂點的直角三角形,且斜邊的中點在y軸上?如果存在,求a的取值范圍;如果不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年甘肅省高三上學期第一次檢測文科數學試卷(解析版) 題型:解答題
(本小題滿分10分)選修4-5:不等式選講
設函數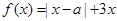 ,其中
,其中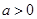 .
.
(I)當a=1時,求不等式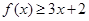 的解集.
的解集.
(II)若不等式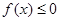 的解集為{x|
的解集為{x|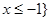 ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中數學 來源:河北省衡水中學2011-2012學年高三下學期一調考試(數學文) 題型:解答題
選修4-5:不等式選講
設函數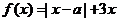 ,其中
,其中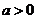 .
.
(I)當a=1時,求不等式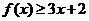 的解集.
的解集.
(II)若不等式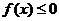 的解集為{x|
的解集為{x|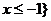 ,求a的值.
,求a的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com