已知數列
和
滿足：
.且是以q為公比的等比數列.
（Ⅰ）證明：
;
（Ⅱ）若
，證明數例
是等比數例;
（Ⅲ）求和：
…
.
科目：高中數學 來源： 題型：
（本小題滿分12分）
已知數列
、
滿足: 
為常數), 且
。
(Ⅰ)若是等比數列, 求數列和前
項和
；
(Ⅱ)當是等比數列時, 甲同學說: 一定是等比數列; 乙 同學說: 一定不是等比數列, 請你對甲、乙兩人的判斷正確與否作出解釋
查看答案和解析>>
科目：高中數學 來源：2013屆度寧夏高二下學期期中考試理科數學試卷（解析版） 題型：解答題
（12分）
已知數列{an}滿足a1=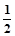
，且前n項和Sn滿足：Sn=n2an，求a2,a3,a4,猜想{an}的通項公式，并加以證明。
查看答案和解析>>
科目：高中數學 來源：2010-2011學年上海市閘北區高三第一學期期末數學理卷 題型：解答題
（滿分20分）本題有2小題，第1小題12分，第2小題8分．
已知數列{
}和{
}滿足：對于任何
，有
，
為非零常數），且
．
（1）求數列{}和{}的通項公式；
（2）若
是
與
的等差中項，試求
的值，并研究：對任意的，是否一定能是數列{}中某兩項（不同于）的等差中項，并證明你的結論．
查看答案和解析>>
科目：高中數學 來源：2010年廣東省高二上學期期中考試數學卷 題型：解答題
（本小題滿分14分） 已知數列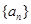
和
滿足：
，
，
，
（
），且是以
為公比的等比數列．
（Ⅰ）證明：
；
（Ⅱ）若
，證明：數列
是等比數列；
（Ⅲ）（理科做，文科不做）若
，求和：
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，有
，
．
，
，
，
．
是首項為5，以
為公比的等比數列．
，
，于是
．
時，
．
時，
．
，又
，
，
，
，
．
．
和
滿足：
，
，
，
（
），且
為公比的等比數列．
；
，證明數列
是等比數列；
．