
 <y<π且sin(x+y)=
<y<π且sin(x+y)=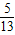
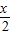 =
= ,分別求cosx及cosy的值;
,分別求cosx及cosy的值;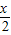 的范圍,由tan
的范圍,由tan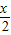 的值,利用同角三角函數間的基本關系即可求出cos
的值,利用同角三角函數間的基本關系即可求出cos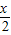 的值,進而再利用同角三角函數間的基本關系求出sin
的值,進而再利用同角三角函數間的基本關系求出sin 的值,利用二倍角的正弦、余弦函數公式,由sin
的值,利用二倍角的正弦、余弦函數公式,由sin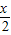 和cos
和cos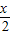 的值及x的范圍,即可求出sinx和cosx的值,再根據x與y的范圍得到x+y的范圍,由sin(x+y)的值,利用同角三角函數間的基本關系求出cos(x+y)的值,然后把y變為(x+y)-x,利用兩角差的余弦函數公式化簡后,將各自的值代入即可求出值;
的值及x的范圍,即可求出sinx和cosx的值,再根據x與y的范圍得到x+y的范圍,由sin(x+y)的值,利用同角三角函數間的基本關系求出cos(x+y)的值,然后把y變為(x+y)-x,利用兩角差的余弦函數公式化簡后,將各自的值代入即可求出值;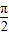 <y<π,tan
<y<π,tan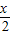 =
= ,且0<
,且0<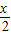 <
<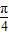 ,
,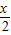 =
=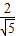 ,sin
,sin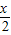 =
=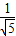 ,
,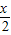 -1=
-1= ,sinx=
,sinx= ,
,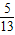 ,
,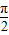 <x+y<
<x+y<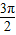 ,
,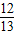 ,
,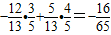 ;
; <y<π,
<y<π,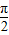 <x+y<
<x+y<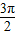 ,
,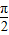 <y<x+y<
<y<x+y<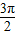 ,
,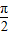 ,
,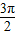 ]上為減函數,
]上為減函數,

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:高中數學全解題庫(國標蘇教版·必修4、必修5) 蘇教版 題型:044
已知0<x<![]() <y<π,且sin(x+y)=
<y<π,且sin(x+y)=![]() .
.
(1)若![]() ,求cosx及cosy的值;
,求cosx及cosy的值;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
(1)若tan![]() =
=![]() ,分別求出cosx及cosy的值;
,分別求出cosx及cosy的值;
(2)試比較siny與sin(x+y)的大小,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 <y<π且sin(x+y)=
<y<π且sin(x+y)=
 =
= ,分別求cosx及cosy的值;
,分別求cosx及cosy的值;查看答案和解析>>
科目:高中數學 來源: 題型:
(1)若tan![]() =
=![]() ,分別求出cosx、cosy的值;
,分別求出cosx、cosy的值;
(2)試比較siny與sin(x+y)的大小,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com