
已知定義域為R的函數f(x)滿足f(f(x)-x2+x)=f(x)-x2+x.
(Ⅰ)若f(2)=3,求f(1);又若f(0)=a,求f(a);
(Ⅱ)設有且僅有一個實數x0,使得f(x0)= x0,求函數f(x)的解析表達式.
解:(Ⅰ)因為對任意x∈R,有f(f(x)-x2 + x)=f(x)- x2 +x,
所以f(f(2)- 22+2)=f(2)-22+2.
又由f(2)=3,得f(3-22+2)-3-22+2,即f(1)=1.
若f(0)=a,則f(a-02+0)=a-02+0,即f(a)=a.
(Ⅱ)因為對任意x∈R,有f(f(x))-x2 +x)=f(x)-x2 +x.
又因為有且只有一個實數x0,使得f(x0)- x0.所以對任意xεR,有f(x)-x2 +x= x0.
在上式中令x= x0,有f(x0)-x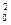 + x0= x0,
+ x0= x0,
又因為f(x0)- x0,所以x0-x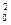 =0,故x0=0或x0=1.
=0,故x0=0或x0=1.
若x0=0,則f(x)- x2 +x=0,即f(x)= x2-x.
但方程x2-x=x有兩上不同實根,與題設條件矛質,故x2≠0.
若x2=1,則有f(x)-x2 +x=1,即f(x)= x2-x+1.易驗證該函數滿足題設條件.
綜上,所求函數為f(x)= x2-x+1(x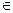 R)
R)
解析


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
已知函數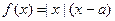 ,
,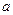 為實數.
為實數.
(1)當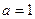 時,判斷函數
時,判斷函數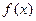 的奇偶性,并說明理由;
的奇偶性,并說明理由;
(2)當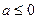 時,指出函數
時,指出函數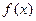 的單調區間(不要過程);
的單調區間(不要過程);
(3)是否存在實數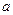
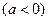 ,使得
,使得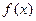 在閉區間
在閉區間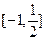 上的最大值為2.若存在,求出
上的最大值為2.若存在,求出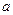 的值;若不存在,請說明理由
的值;若不存在,請說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某企業生產一種產品時,固定成本為5 000元,而每生產100臺產品時直接消耗成本要增加2 500元,市場對此商品年需求量為500臺,銷售的收入函數為
500元,市場對此商品年需求量為500臺,銷售的收入函數為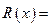
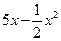 (萬元)(0≤
(萬元)(0≤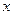 ≤5),其中
≤5),其中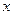 是產品售出的數量(單位:百臺)
是產品售出的數量(單位:百臺)
(1)把利潤表示為年產量的函數;(2)年產量多少時,企業所得的利潤最大;
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題13分)已知函數 與
與 的圖象相交于
的圖象相交于 ,
, ,
, ,
, 分別是
分別是 的圖象在
的圖象在 兩點的切線,
兩點的切線, 分別是
分別是 ,
, 與
與 軸的交點.
軸的交點.
(1)求 的取值范圍;
的取值范圍;
(2)設 為點
為點 的橫坐標,當
的橫坐標,當 時,寫出
時,寫出 以
以 為自變量的函數式,并求其定義域和值域;
為自變量的函數式,并求其定義域和值域;
(3)試比較 與
與 的大小,并說明理由(
的大小,并說明理由( 是坐標原點).
是坐標原點).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)已知二次函數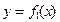 的
的 圖象以原點為頂點且過點(1,1),反比例函數
圖象以原點為頂點且過點(1,1),反比例函數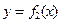 的圖象與直線
的圖象與直線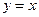 的兩個交點間的距離為8,
的兩個交點間的距離為8,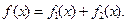
(1)求函數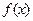 的表達式;
的表達式;
(2)證明:當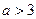 時,關于
時,關于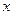 的方程
的方程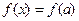 有三個實數解.
有三個實數解.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定義域為區間[-1,1].
(1)求g(x)的解析式;
(2)判斷g(x)的單調性.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com