
 .
. 的值及函數(shù)
的值及函數(shù)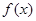 的單調遞增區(qū)間;
的單調遞增區(qū)間; 在區(qū)間
在區(qū)間 上的最大值和最小值.
上的最大值和最小值. 同步奧數(shù)系列答案
同步奧數(shù)系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
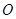 為中心,正北方向和正東方向的馬路為邊界的扇形地域內建造一個圖書館.為了充分利用這塊土地,并考慮與周邊環(huán)境協(xié)調,設計要求該圖書館底面矩形的四個頂點都要在邊界上,圖書館的正面要朝市政府大樓.設扇形的半徑
為中心,正北方向和正東方向的馬路為邊界的扇形地域內建造一個圖書館.為了充分利用這塊土地,并考慮與周邊環(huán)境協(xié)調,設計要求該圖書館底面矩形的四個頂點都要在邊界上,圖書館的正面要朝市政府大樓.設扇形的半徑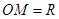 ,
, ,
, 與
與 之間的夾角為
之間的夾角為 .
.
 的面積
的面積 表示成
表示成 的函數(shù).
的函數(shù). 為何值時,矩形
為何值時,矩形 的面積
的面積 有最大值?其最大值是多少?(用含R的式子表示)
有最大值?其最大值是多少?(用含R的式子表示)查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
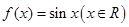 與
與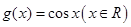 .
.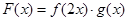 ,有下列結論:①
,有下列結論:①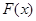 是奇函數(shù);②
是奇函數(shù);②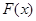 是周期函數(shù),最小正周期為
是周期函數(shù),最小正周期為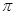 ;③
;③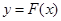 的圖象關于點
的圖象關于點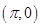 對稱;④
對稱;④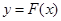 的圖象關于直線
的圖象關于直線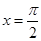 對稱.其中正確結論的序號是__________;(直接寫出所有正確結論的序號)
對稱.其中正確結論的序號是__________;(直接寫出所有正確結論的序號)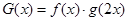 ,求滿足
,求滿足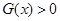 的
的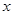 的取值范圍;
的取值范圍;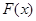 的值域為
的值域為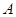 ,函數(shù)
,函數(shù)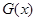 的值域為
的值域為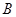 ,試判斷集合
,試判斷集合 之間的關系.
之間的關系.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
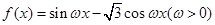 的圖象與
的圖象與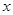 軸的兩個相鄰交點的距離等于
軸的兩個相鄰交點的距離等于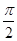 ,若將函數(shù)
,若將函數(shù)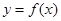 的圖象向左平移
的圖象向左平移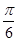 個單位得到函數(shù)
個單位得到函數(shù)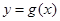 的圖象,則
的圖象,則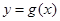 是減函數(shù)的區(qū)間為( )
是減函數(shù)的區(qū)間為( )A. | B. | C. | D. |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 -
- sin2ωx-sinωxcosωx(ω>0),且y=f(x)圖象的一個對稱中心到最近的對稱軸的距離為
sin2ωx-sinωxcosωx(ω>0),且y=f(x)圖象的一個對稱中心到最近的對稱軸的距離為 .
. ]上的最大值和最小值.
]上的最大值和最小值.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
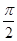 )的部分圖象如圖所示,則( )
)的部分圖象如圖所示,則( )
A.ω=2,φ= | B.ω=1,φ=- |
C.ω=1,φ= | D.ω=2,φ=- |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com