
用反證法證明命題:“若a,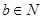 ,
,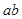 能被5整除,則a,b中至少有一個能被5整除”,那么假設的內容是( )
能被5整除,則a,b中至少有一個能被5整除”,那么假設的內容是( )
| A.a,b都能被5整除 | B.a,b都不能被5整除 |
| C.a,b有一個能被5整除 | D.a,b有一個不能被5整除 |
科目:高中數學 來源: 題型:單選題
給出命題:若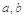 是正常數,且
是正常數,且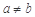 ,
,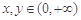 ,則
,則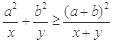 (當且僅當
(當且僅當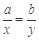 時等號成立).根據上面命題,可以得到函數
時等號成立).根據上面命題,可以得到函數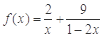 (
(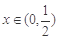 )的最小值及取最小值時的
)的最小值及取最小值時的 值分別為( )
值分別為( )
A.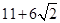 , ,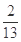 | B.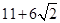 , ,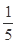 |
C.25,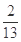 | D.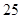 , ,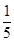 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
將正偶數 、
、 、
、 、
、 、
、 按表
按表 的方式進行排列,記
的方式進行排列,記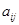 表示第
表示第 行和第
行和第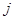 列的數,若
列的數,若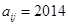 ,則
,則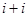 的值為( )
的值為( )
| | 第 列 列 | 第 列 列 | 第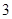 列 列 | 第 列 列 | 第 列 列 |
第 行 行 | |  |  |  |  |
第 行 行 |  | 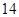 |  |  | |
第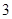 行 行 | | 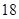 | 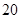 | 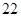 | 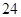 |
第 行 行 | 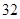 |  | 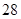 | 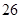 | |
第 行 行 | |  | 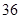 | 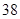 | 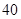 |
 |  |  |  |  |  |
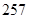 B.
B.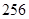 C.
C.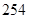 D.
D.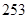
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
用數學歸納法證明“n3+(n+1)3+(n+2)3(n∈N*)能被9整除”,要利用歸納假設證n=k+1時的情況,只需展開( )
| A.(k+3)3 | B.(k+2)3 |
| C.(k+1)3 | D.(k+1)3+(k+2)3 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
觀察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,則a10+b10=( )
| A.28 | B.76 | C.123 | D.199 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
有兩種花色的正六邊形地面磚,按下圖的規律拼成若干個圖案,則第六個圖案中有菱形紋的正六邊形的個數是( ).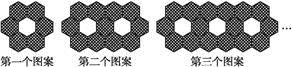
| A.26 | B.31 | C.32 | D.36 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
已知n是正偶數,用數學歸納法證明時,若已假設n=k(k≥2且為偶數)時命題為真,則還需證明( )
| A.n=k+1時命題成立 |
| B.n=k+2時命題成立 |
| C.n=2k+2時命題成立 |
| D.n=2(k+2)時命題成立 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com