
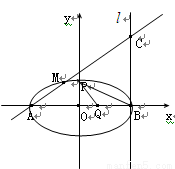
(理)如圖,|AB|=2,O為AB中點,直線 過B且垂直于AB,過A的動直線與
過B且垂直于AB,過A的動直線與 交于點C,點M在線段AC上,滿足
交于點C,點M在線段AC上,滿足 =
= .
.

(1)求點M的軌跡方程;
(2)若過B點且斜率為-  的直線與軌跡M交于點P,點Q(t,0)是x軸上任意一點,求當ΔBPQ為銳角三角形時t的取值范圍.
的直線與軌跡M交于點P,點Q(t,0)是x軸上任意一點,求當ΔBPQ為銳角三角形時t的取值范圍.
(理)(1)得x2+4y2=1(y≠0);
(2) - 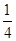 <t<0
。
<t<0
。
【解析】設(shè)M(x,y),C(1,y0),然后再此條件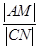 =
=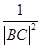 坐標化可得
坐標化可得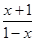 =
=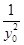 ,
,
再根據(jù)A、M、C三點一線,∴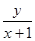 =
=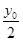 ,然后兩式聯(lián)立消去y0,即可得到點M的軌跡方程.要注意
,然后兩式聯(lián)立消去y0,即可得到點M的軌跡方程.要注意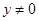 .
.
(2)用向量判定是銳角的條件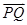 ·
·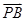 >0,并且
>0,并且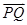 和
和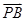 不共線,然后用坐標表示出來,即可得到t的取值范圍.
不共線,然后用坐標表示出來,即可得到t的取值范圍.
(理)(1)設(shè)M(x,y),C(1,y0),∵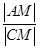 =
=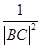 ,∴
,∴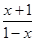 =
=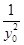 (2’)
(2’)
又A、M、C三點一線,∴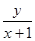 =
=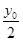 ②
(4’)
②
(4’)
由(1)、(2)消去y0,得x2+4y2=1(y≠0) (6’)
(2)P(0, 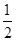 )是軌跡M短軸端點,∴t≥0時∠PQB或∠PBQ不為銳角,∴t<0
)是軌跡M短軸端點,∴t≥0時∠PQB或∠PBQ不為銳角,∴t<0
又∠QPB為銳角,∴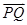 ·
·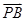 >0,∴(t,-
>0,∴(t,- 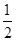 )(1,-
)(1,-
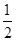 )=t+
)=t+
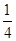 >0,∴-
>0,∴- 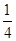 <t<0
(12’)
<t<0
(12’)


 53隨堂測系列答案
53隨堂測系列答案科目:高中數(shù)學 來源: 題型:
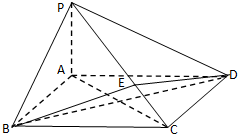 (理)如圖所示,在四棱錐P-ABCD中,底面ABCD為正方形,PA⊥平面ABCD,點 E在線段PC上,設(shè)
(理)如圖所示,在四棱錐P-ABCD中,底面ABCD為正方形,PA⊥平面ABCD,點 E在線段PC上,設(shè)| PE | EC |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
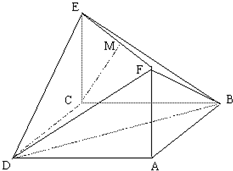 (理)如圖,已知矩形ACEF的邊CE與正方形ABCD所在平面垂直,AB=
(理)如圖,已知矩形ACEF的邊CE與正方形ABCD所在平面垂直,AB=| 2 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
 (理)如圖,四棱錐P-ABCD的底面是矩形,PA⊥面ABCD,PA=2
(理)如圖,四棱錐P-ABCD的底面是矩形,PA⊥面ABCD,PA=2| 19 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(08年浙江卷理)如圖,AB是平面![]() 的斜線段,A為斜足,若點P在平面
的斜線段,A為斜足,若點P在平面![]() 內(nèi)運動,使得△ABP的面積為定值,則動點P的軌跡是( )
內(nèi)運動,使得△ABP的面積為定值,則動點P的軌跡是( )

(A)圓 (B)橢圓
(C)一條直線 (D)兩條平行直線
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com