
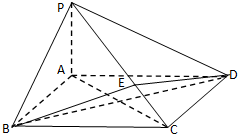
 (理)如圖所示,在四棱錐P-ABCD中,底面ABCD為正方形,PA⊥平面ABCD,點 E在線段PC上,設
(理)如圖所示,在四棱錐P-ABCD中,底面ABCD為正方形,PA⊥平面ABCD,點 E在線段PC上,設| PE | EC |
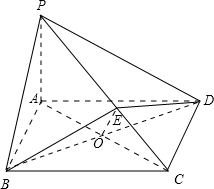 (Ⅰ)證明,如圖,
(Ⅰ)證明,如圖,| 2 |
| ||
| 2 |
| a2+2a2 |
| 3 |
| AC |
| PC |
| EC |
| OC |
| ||
|
| EC | ||||
|
| ||
| 3 |
| PE |
| EC |
| PC-EC |
| EC |
| ||||
|
| OC2-EC2 |
(
|
| ||
| 6 |
| BO |
| OE |
| ||||
|
| 3 |
| π |
| 3 |


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
(09年濱州一模理)(12分)
如圖所示,在四棱錐P-ABCD中,底面ABCD是邊長為2的正方形,平面PBC⊥底面ABCD,且PB=PC=![]() .
.
(Ⅰ)求證:AB⊥CP;
(Ⅱ)求點![]() 到平面
到平面![]() 的距離;
的距離;
(Ⅲ)設面![]() 與面
與面![]() 的交線為
的交線為![]() ,求二面角
,求二面角![]() 的大小.
的大小.

查看答案和解析>>
科目:高中數學 來源: 題型:
(08年四校聯考二理) 如圖所示,設點F坐標為 (1 , 0 ),點P在y軸上運動,點M在x軸運動上,其中![]() ?
?![]() =0,若動點N滿足條件
=0,若動點N滿足條件![]()
![]()
(Ⅰ)求動點N的軌跡![]() 的方程;
的方程;
(Ⅱ)過點F(1 , 0 )的直線l和![]() 分別與曲線
分別與曲線![]() 交于A、B兩點和C、D兩點,若
交于A、B兩點和C、D兩點,若![]() ,試求四邊形ACBD的面積的最小值.
,試求四邊形ACBD的面積的最小值.

查看答案和解析>>
科目:高中數學 來源: 題型:
(08年內江市三模理) 如圖所示是2008年北京奧運會的會徽,其中的“中國印”由四個不連通的色塊組成,可以用線段在不穿越其它色塊的條件下將其中兩個色塊連接(如同架橋),如果用三條線段將四個色塊連接起來,不同的連接方法有_______種。
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()

查看答案和解析>>
科目:高中數學 來源:2011-2012學年黑龍江省龍東南七校聯考高一(下)期末數學試卷(解析版) 題型:填空題
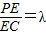 ,PA=AB.
,PA=AB.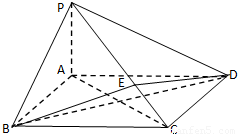
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com