
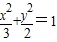 相交與M、N兩點
相交與M、N兩點 方程,并將其化為一個關于t的一元二次方程,根據|PM|•|PN|=|t1•t2|,結合韋達定理和余弦函數的性質,即可求出PM•PN的最小值.
方程,并將其化為一個關于t的一元二次方程,根據|PM|•|PN|=|t1•t2|,結合韋達定理和余弦函數的性質,即可求出PM•PN的最小值.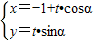 (t為參數)…2分
(t為參數)…2分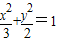 得
得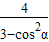 …8分
…8分 …10分
…10分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
| 2 |
| 10 |
| MF1 |
| MF2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com