
設數列 的各項均為正數,其前n項的和為
的各項均為正數,其前n項的和為 ,對于任意正整數m,n,
,對于任意正整數m,n,  恒成立.
恒成立.
(Ⅰ)若 =1,求
=1,求 及數列
及數列 的通項公式;
的通項公式;
(Ⅱ)若 ,求證:數列
,求證:數列 是等比數列.
是等比數列.
(Ⅰ) 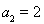 ,
,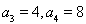 ,
,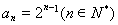 ;(Ⅱ)參考解析
;(Ⅱ)參考解析
【解析】
試題分析:(Ⅰ)通過令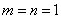 ,可求得
,可求得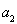 .同理可以求出
.同理可以求出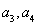 .由于所給的等式中有兩個參數m,n.所以以一個為主元,讓另一個m=1,和m=2取特殊值通過消去
.由于所給的等式中有兩個參數m,n.所以以一個為主元,讓另一個m=1,和m=2取特殊值通過消去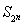 即可得到一個關于
即可得到一個關于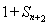 與
與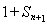 的遞推式.從而可求出
的遞推式.從而可求出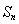 的通項式,從而通過
的通項式,從而通過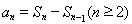 ,可求出通項
,可求出通項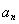 .但前面兩項要驗證是否符合.
.但前面兩項要驗證是否符合.
(Ⅱ)因為已知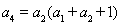 ,所以令
,所以令 .即可求得
.即可求得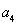 與
與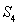 的關系式.再利用
的關系式.再利用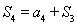 .又得到了一個關于
.又得到了一個關于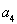 與
與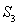 的關系式.從而可得
的關系式.從而可得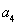 與
與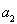 的關系式.又根據
的關系式.又根據 與
與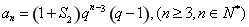 .可求出
.可求出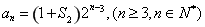 .再根據
.再根據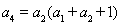 及
及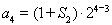 .即可求出結論.最后要驗證前兩項是否成立.
.即可求出結論.最后要驗證前兩項是否成立.
試題解析:(1)由條件,得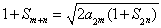 ①
①
在①中,令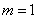 ,得
,得 ②
②
令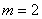 ,得
,得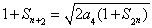 ③
③
③/②得 ,記
,記 ,則數列
,則數列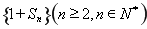 是公比為
是公比為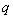 的等比數列。
的等比數列。
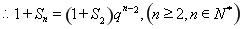 ④
④
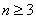 時,
時,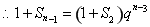 , ⑤
, ⑤
④-⑤,得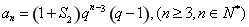
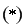 ,當n≥3時,{
,當n≥3時,{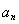 }是等比數列.
}是等比數列.
在①中,令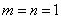 ,得
,得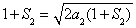 ,從而
,從而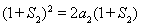 ,則
,則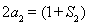 ,所以
,所以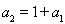 .
.
又因為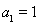 ,所以
,所以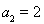 2分
2分
在①中,令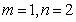 ,得
,得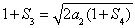 ,則
,則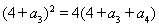 ⑥
⑥
在①中,令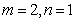 ,得
,得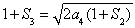 ,則
,則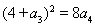 ⑦
⑦
由⑥⑦解得: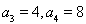 6分
6分
則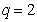 ,由
,由
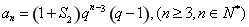 得
得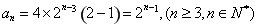
又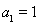 ,
,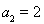 也適應上式,所以
也適應上式,所以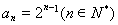 . 8分
. 8分
(2)在①中,令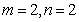 ,得
,得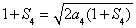 ,則
,則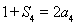 ,所以
,所以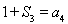 ;
;
在①中,令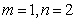 ,得
,得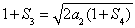 ,則
,則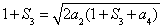 ,所以
,所以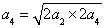 ,則
,則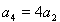 ,
,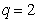 ;代入
;代入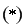 式,得
式,得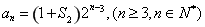 12分
12分
由條件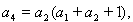 得
得
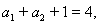 又因
又因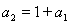 ,所以
,所以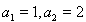
故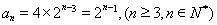 ,
,
因為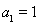 ,
,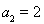 也適應上式,所以
也適應上式,所以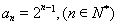
所以數列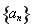 是等比數列. 14分
是等比數列. 14分
考點:1.數列的遞推思想.2.數列通項與前n項和的轉化關系.3.歸納推理的思想.4.消元方程化簡的能力.


 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案科目:高中數學 來源:2012-2013學年山東省濟寧市高三上學期期末模擬理科數學試卷(解析版) 題型:選擇題
設數列 的各項均為正數,前
的各項均為正數,前 項和為
項和為 ,對于任意的
,對于任意的 ,
, 成等差數列,設數列
成等差數列,設數列 的前
的前 項和為
項和為 ,且
,且 ,則對任意的實數
,則對任意的實數 (
( 是自然對數的底)和任意正整數
是自然對數的底)和任意正整數 ,
, 小于的最小正整數為( )
小于的最小正整數為( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2014屆江蘇南通市高一下學期期中數學試卷(解析版) 題型:解答題
設數列 的各項均為正數.若對任意的
的各項均為正數.若對任意的 ,存在
,存在 ,使得
,使得 成立,則稱數列
成立,則稱數列 為“Jk型”數列.
為“Jk型”數列.
(1)若數列 是“J2型”數列,且
是“J2型”數列,且 ,
, ,求
,求 ;
;
(2)若數列 既是“J3型”數列,又是“J4型”數列,證明:數列
既是“J3型”數列,又是“J4型”數列,證明:數列 是等比數列.
是等比數列.
【解析】1)中由題意,得 ,
, ,
, ,
, ,…成等比數列,且公比
,…成等比數列,且公比 ,
,
所以.
(2)中證明:由{ }是“j4型”數列,得
}是“j4型”數列,得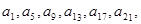 ,…成等比數列,設公比為t. 由{
,…成等比數列,設公比為t. 由{ }是“j3型”數列,得
}是“j3型”數列,得
 ,…成等比數列,設公比為
,…成等比數列,設公比為 ;
;
 ,…成等比數列,設公比為
,…成等比數列,設公比為 ;
;
 …成等比數列,設公比為
…成等比數列,設公比為 ;
;
查看答案和解析>>
科目:高中數學 來源:2010-2011學年吉林省高三沖刺考試數學文卷 題型:解答題
(本小題滿分12分)
設數列 的各項均為正數,若對任意的正整數
的各項均為正數,若對任意的正整數 ,都有
,都有 成等差數列,且
成等差數列,且 成等比數列.
成等比數列.
(Ⅰ)求證數列 是等差數列;
是等差數列;
(Ⅱ)如果 ,求數列錯誤!不能通過編輯域代碼創建對象。的前錯誤!不能通過編輯域代碼創建對象。項和。
,求數列錯誤!不能通過編輯域代碼創建對象。的前錯誤!不能通過編輯域代碼創建對象。項和。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com