中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情
橢圓C1：
x2
a2
+
y2
b2
=1（a＞b＞0）的長軸長為4，焦距為2，F1、F2分別為橢圓的左、右焦點，直線l1過點F1且垂直于橢圓的長軸，動直線l2垂直l1于點P，線段PF2垂直平分線交l2于點M
（1）求橢圓C1的標準方程和動點M的軌跡C2的方程．
（2）過橢圓C1的右焦點F2作斜率為1的直線交橢圓于A、B兩點，求△ABF1的面積．
（3）設軌跡C2與x軸交于點Q，不同的兩點R、S在軌跡C2上，
滿足
QR
•
QS
=0求證：直線RS恒過x軸上的定點．
分析：（1）由題設知：2a=4，即a=2，2c=2，即c=1，b2=a2-c2=3，故橢圓方程為
x2
4
+
y2
3
=1，由MP=MF2，知動點M到定直線l1：x=-1，的距離等于它到定點F1（1，0）的距離，由此能求出點M的軌跡C2的方程．
（2）
x2
4
+
y2
3
=1
y=x-1
消去x并整理得：7y2+6y-9=0，設A（x3，y3），B（x4，y4）則y3+y4=-
6
7
，y3y4=-
9
7
，由此能求出△ABF1的面積．
（3）Q（0，0），設R(
y12
4
，y1)  ，S(
y22
4
，y2)，kRS=
y2-y1
y22
4
-
y21
4
=
4
y1+y2
，由
QR
•
QS
=0，知
y
2
1
y
2
2
16
+y1y2=0，由題設知直線RS恒過定點（4，0）．
解答：解：（1）由題設知：2a=4，即a=2，2c=2，即c=1，b2=a2-c2=3，故橢圓方程為
x2
4
+
y2
3
=1，由MP=MF2，知
∴動點M到定直線l1：x=-1，的距離等于它到定點F1（1，0）的距離，
∴動點M的軌跡是C為l1準線，F2為焦點的拋物線
∴點M的軌跡C2的方程為y2=4x（5分）
（2）
x2
4
+
y2
3
=1
y=x-1
消去x并整理得：7y2+6y-9=0
設A（x3，y3），B（x4，y4）則y3+y4=-
6
7
，y3y4=-
9
7
（7分）S△ABF1=
1
2
|F1F2|•|y3-y4|=|y3-y4|=
(y3+y4)2-4y3y4
=
12
2
7
（9分）
（3）Q（0，0），設R(
y12
4
，y1)  ，S(
y22
4
，y2)，kRS=
y2-y1
y22
4
-
y21
4
=
4
y1+y2
（10分）∵
QR
•
QS
=0∴
y
2
1
y
2
2
16
+y1y2=0∵y1≠0，y2≠0∴y1y2=-16x1x2=16（11分）∴直線RS：y-y1=
4
y1+y2
(x-x1)∴y=
4
y1+y2
x+y1-
4x1
y1+y2
∴y=
4
y1+y2
x+
y1(y1+y2)-4x1
y1+y2
=
4
y1+y2
x+
y
2
1
+y1y2-4•
y
2
1
4
y1+y2
=
4
y1+y2
x+
y1y2
y1+y2
=
4
y1+y2
x+
-16
y1+y2
=
4
y1+y2
(x-4)（13分）
故直線RS恒過定點（4，0）（14分）
點評：本題考查直線和圓錐曲線的位置關系，解題時要認真審題，注意合理地進行等價轉化．
練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

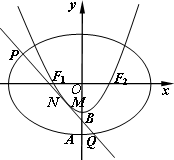精英家教網設橢圓C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦點分別是F1、F2，下頂點為A，線段OA的中點為B（O為坐標原點），如圖．若拋物線C2：y=x2-1與y軸的交點為B，且經過F1，F2點．
（Ⅰ）求橢圓C1的方程；
（Ⅱ）設M（0，-
4
5
），N為拋物線C2上的一動點，過點N作拋物線C2的切線交橢圓C1于P、Q兩點，求△MPQ面積的最大值．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知橢圓C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦點F2與拋物線C2：y2=4x的焦點重合，橢圓C1與拋物線C2在第一象限的交點為P，|PF2|=
5
3
，求橢圓C1的方程．

查看答案和解析>>

科目：高中數學 來源： 題型：

（2013•三門峽模擬）已知橢圓C1：
x2
a2
+
y2
b2
=1（a＞b＞0）的長軸長為4，離心率為
1
2
，F1、F2分別為其左右焦點．一動圓過點F2，且與直線x=-1相切．
（Ⅰ）（ⅰ）求橢圓C1的方程； （ⅱ）求動圓圓心C軌跡的方程；
（Ⅱ）在曲線上C有兩點M、N，橢圓C1上有兩點P、Q，滿足MF2與
NF2
共線，
PF2
與
QF2
共線，且
PF2
•
MF2
=0，求四邊形PMQN面積的最小值．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知橢圓C1：
x2
A2
+
y2
B2
=1(A＞B＞0)和雙曲線C2：
x2
a2
-
y2
b2
=1(a＞0，b＞0)有相同的焦點F1、F2，2c是它們的共同焦距，且它們的離心率互為倒數，P是它們在第一象限的交點，當cos∠F1PF2=60°時，下列結論中正確的是（　　）

查看答案和解析>>

科目：高中數學 來源： 題型：

（2013•汕頭一模）已知橢圓C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦點分別為F1、F2，右頂點為A，離心率e=
1
2

（1）設拋物線C2：y2=4x的準線與x軸交于F1，求橢圓的方程；
（2）設已知雙曲線C3以橢圓C1的焦點為頂點，頂點為焦點，b是雙曲線C3在第一象限上任意-點，問是否存在常數λ（λ＞0），使∠BAF1=λ∠BF1A恒成立？若存在，求出λ的值；若不存在，請說明理由．

查看答案和解析>>

同步練習冊答案