
�O(sh��)����(sh��) ��
��
��1����(sh��) ����С�����ں͆��{(di��o)�f���^(q��)�g��
����С�����ں͆��{(di��o)�f���^(q��)�g��
��2����(d��ng) �r(sh��)��
�r(sh��)�� �����ֵ��2����
�����ֵ��2���� ��ֵ�������
��ֵ������� �Č�(du��)�Q(ch��ng)�S���̣�
�Č�(du��)�Q(ch��ng)�S���̣�
��1��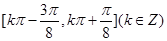 ����2��
����2�� ��
�� �Č�(du��)�Q(ch��ng)�S���̞�
�Č�(du��)�Q(ch��ng)�S���̞�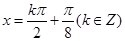 ��
��
����ԇ�}��������1����(sh��) �Ć��{(di��o)�f�p�^(q��)�g�����Ȍ�(du��)
�Ć��{(di��o)�f�p�^(q��)�g�����Ȍ�(du��) �M(j��n)�к��׃��������׃?y��u)�һ��(g��)�ǵ�һ��(g��)���Ǻ���(sh��)��Ȼ���������Ǻ���(sh��)�Ć��{(di��o)�ԣ���(l��i)��(sh��)
�M(j��n)�к��׃��������׃?y��u)�һ��(g��)�ǵ�һ��(g��)���Ǻ���(sh��)��Ȼ���������Ǻ���(sh��)�Ć��{(di��o)�ԣ���(l��i)��(sh��) �Ć��{(di��o)�f�p�^(q��)�g�����}����ͨ�^(gu��)���繫ʽ���磬�����ǹ�ʽ���õ�
�Ć��{(di��o)�f�p�^(q��)�g�����}����ͨ�^(gu��)���繫ʽ���磬�����ǹ�ʽ���õ� �c
�c ���P(gu��n)ϵʽ�������ÃɽǺ͵����Ǻ���(sh��)��ʽ���õ�
���P(gu��n)ϵʽ�������ÃɽǺ͵����Ǻ���(sh��)��ʽ���õ�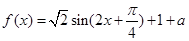 ���Ķ��õ����{(di��o)�f���^(q��)�g����2����
���Ķ��õ����{(di��o)�f���^(q��)�g����2����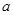 ��ֵ������֪��(d��ng)
��ֵ������֪��(d��ng) �r(sh��)��
�r(sh��)�� �����ֵ��2����
�����ֵ��2���� ����
����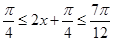 ����(d��ng)
����(d��ng)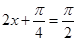 ����
����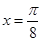 ��
��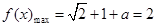 ������
������ ��ֵ����
��ֵ���� �Č�(du��)�Q(ch��ng)�S���̣���
�Č�(du��)�Q(ch��ng)�S���̣���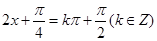 �����
�����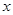 �����Ì�(du��)�Q(ch��ng)�S���̣�
�����Ì�(du��)�Q(ch��ng)�S���̣�
ԇ�}��������1��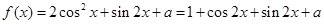
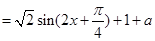 2��
2��
�t ����������
����������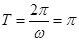 �� 4��
�� 4��
�Ү�(d��ng)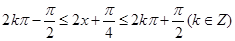 �r(sh��)
�r(sh��) ���{(di��o)�f����
���{(di��o)�f����
�� ��
�� ���{(di��o)�f���^(q��)�g
���{(di��o)�f���^(q��)�g
����(xi��)���_(k��i)�^(q��)�g���۷֣��� 6��
��2����(d��ng) �r(sh��)
�r(sh��)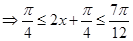 ����(d��ng)
����(d��ng)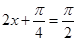 ����
����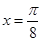 �r(sh��)
�r(sh��)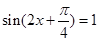 ��
��
���� �� 9��
�� 9��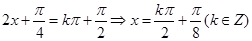 ��
�� ��(du��)�Q(ch��ng)�S�� 12��
��(du��)�Q(ch��ng)�S�� 12��
���c(di��n)�������ǵ����ң��ɽǺ��c������Һ���(sh��)������(sh��) �ĈD���c���|(zh��)��
�ĈD���c���|(zh��)��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�O(sh��)a�� ��b��(4sinx��cosx��sinx)��f(x)��a��b.
��b��(4sinx��cosx��sinx)��f(x)��a��b.
(1)��(sh��)f(x)�Ľ���ʽ��
(2)��֪����(sh��)�أ�0����y��f(��x)�څ^(q��)�g ����������(sh��)����ص�ȡֵ������
����������(sh��)����ص�ȡֵ������
(3)�O(sh��)����A�� ��B��{x||f(x)��m|��2}����A
��B��{x||f(x)��m|��2}����A B����(sh��)��(sh��)m��ȡֵ������
B����(sh��)��(sh��)m��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪����(sh��)f(x)=sin(2x+ ).
).
(1)��(sh��)y=f(x)���{(di��o)�f�p�^(q��)�g.
(2)��(hu��)������(sh��)y=f(x)�څ^(q��)�g[0,��]�ϵĈD��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪a>0,����(sh��)f(x)=-2asin(2x+ )+2a+b,��(d��ng)x��[0,
)+2a+b,��(d��ng)x��[0, ]�r(sh��),-5��f(x)��1.
]�r(sh��),-5��f(x)��1.
(1)��(sh��)a,b��ֵ.
(2)�O(sh��)g(x)=f(x+ )��lg g(x)>0,��g(x)���{(di��o)�^(q��)�g.
)��lg g(x)>0,��g(x)���{(di��o)�^(q��)�g.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪����(sh��) �� �IJ��ֈD����D��ʾ�������c(di��n)
�� �IJ��ֈD����D��ʾ�������c(di��n) �LjD���һ��(g��)����c(di��n).
�LjD���һ��(g��)����c(di��n).
��1����(sh��) �Ľ���ʽ��
�Ľ���ʽ��
��2����֪ ��
�� ����
���� ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D��ij�@�ֆ�λ��(zh��n)��G��һ�Kֱ����BC�İ�A�οյأ���ABC��ĵط��N�ݣ���ABC�ă�(n��i)��������PQRS��һˮ�أ�����ĵط��N������BC��a����ABC�������O(sh��)��ABC����e��S1�������ε�PQRS��e��S2.
(1)��a������ʾS1��S2��
(2)��(d��ng)a�̶�����׃���r(sh��)���� ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪
��1������(ji��n) ��
��
��2���� �ǵ������ǣ���
�ǵ������ǣ��� ����
���� ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪����(sh��)f(x)��2sin ��x��cos ��x��2 cos2��x��
cos2��x�� (������>0)���Һ���(sh��)f(x)�����ڞ��.
(������>0)���Һ���(sh��)f(x)�����ڞ��.
(1)������ֵ��
(2)������(sh��)y��f(x)�ĈD������ƽ�� ��(g��)��λ�L(zh��ng)�ȣ��ٌ����ÈD����c(di��n)�ęM����(bi��o)�sС��ԭ��(l��i)��
��(g��)��λ�L(zh��ng)�ȣ��ٌ����ÈD����c(di��n)�ęM����(bi��o)�sС��ԭ��(l��i)�� ��(�v����(bi��o)��׃)�õ�����(sh��)y��g(x)�ĈD����(sh��)g(x)��
��(�v����(bi��o)��׃)�õ�����(sh��)y��g(x)�ĈD����(sh��)g(x)�� �ϵĆ��{(di��o)�^(q��)�g��
�ϵĆ��{(di��o)�^(q��)�g��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪����(sh��) ���g��
���g��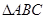 ����
���� ��(du��)߅��
��(du��)߅�� ���Ľ�
���Ľ� �M��
�M�� .
.
������(sh��) ���{(di��o)�f���^(q��)�g��
���{(di��o)�f���^(q��)�g��
������ ����
���� .
.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com