
某地區為了解高二學生作業量和玩電腦游戲的情況,對該地區內所有高二學生采用隨機抽樣的方法,得到一個容量為200的樣本.統計數據如下:
(1)已知該地區共有高二學生42500名,根據該樣本估計總體,其中喜歡電腦游戲并認為作業不多的人有多少名?
(2)在A,B,C,D,E,F六名學生中,僅有A,B兩名學生認為作業多.如果從這六名學生中隨機抽取兩名,求至少有一名學生認為作業多的概率.
(1)7650名;(2)
解析試題分析:(1)利用樣本估計總體,可求得喜歡電腦游戲并認為作業不多的人數;(2)用列舉法,并利用古典概型即可求得至少有一名學生認為作業多的概率
試題解析:(1)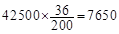 (名) 5分
(名) 5分
(2)【方法一】從這六名學生中隨機抽取兩名的基本事件有:{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F}共15個 7分
其中至少有一個學生認為作業多的事件有{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F}共9個 9分
∴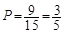
即至少有一名學生認為作業多的概率為 . 12分
. 12分
【方法二】6名學生中隨機抽取2名的選法有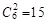 種, 7分
種, 7分
其中至少有一名學生認為作業多的選法有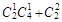 =9種, 9分
=9種, 9分
∴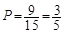
即至少有一名學生認為作業多的概率為 . 12分
. 12分
【方法三】6名學生中隨機抽取2名的選法有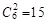 種, 7分
種, 7分
其中沒有人認為作業多的選法有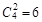 種 9分
種 9分
∴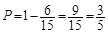
即至少有一名學生認為作業多的概率為 . 12分
. 12分
考點:統計,隨機抽樣,用樣本估計總體,古典概型.


科目:高中數學 來源: 題型:解答題
在平面 內,不等式
內,不等式 確定的平面區域為
確定的平面區域為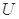 ,不等式組
,不等式組 確定的平面區域為
確定的平面區域為 .
.
(1)定義橫、縱坐標為整數的點為“整點”.在區域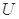 任取3個整點,求這些整點中恰有2個整點在區域
任取3個整點,求這些整點中恰有2個整點在區域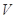 的概率;
的概率;
(2)在區域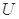 每次任取
每次任取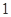 個點,連續取
個點,連續取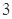 次,得到
次,得到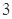 個點,記這
個點,記這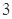 個點在區域
個點在區域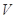 的個數為
的個數為 ,求
,求 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知方程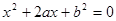 是關于
是關于 的一元二次方程.
的一元二次方程.
(1)若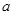 是從集合
是從集合 四個數中任取的一個數,
四個數中任取的一個數,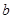 是從集合
是從集合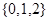 三個數中任取的一個數,求上述方程有實數根的概率;
三個數中任取的一個數,求上述方程有實數根的概率;
(2)若 ,
, ,求上述方程有實數根的概率.
,求上述方程有實數根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
甲、乙兩人各進行3次射擊,甲每次擊中目標的概率為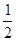 ,乙每次擊中目標的概率
,乙每次擊中目標的概率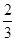 .
.
(1)記甲擊中目標的次數為ξ,求ξ的概率分布列及數學期望Eξ;
(2)求甲恰好比乙多擊中目標2次的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
以下莖葉圖記錄了甲、乙兩組各三名同學在期末考試的數學成績,乙組記錄中有一個數字模糊,無法確認.假設這個數字具有隨機性,并在圖中以a表示.
(1)若甲、乙兩個小組的數學平均成績相同,求a的值;
(2)求乙組平均成績超過甲組平均成績的概率;
(3)當a=2時,分別從甲、乙兩組中各隨機選取一名同學,設這兩名同學成績之差的絕對值為X,求隨機變量X的分布列和數學期望,
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工廠生產A,B兩種元件,其質量按測試指標劃分,指標大于或等于82為正品,小于82為次品.現隨機抽取這兩種元件各100個進行檢測,檢測結果統計如下:
| 測試 指標 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校夏令營有3名男同學 和3名女同學
和3名女同學 ,其年級情況如下表:
,其年級情況如下表:
| | 一年級 | 二年級 | 三年級 |
| 男同學 | A | B | C |
| 女同學 | X | Y | Z |
 為事件“選出的2人來自不同年級且恰有1名男同學和1名女同學”,求事件
為事件“選出的2人來自不同年級且恰有1名男同學和1名女同學”,求事件 發生的概率.
發生的概率.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com