
設 ,兩個函數
,兩個函數 ,
, 的圖像關于直線
的圖像關于直線 對稱.
對稱.
(1)求實數 滿足的關系式;
滿足的關系式;
(2)當 取何值時,函數
取何值時,函數 有且只有一個零點;
有且只有一個零點;
(3)當 時,在
時,在 上解不等式
上解不等式 .
.
(1)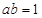 ;(2)
;(2)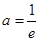 ;(3)
;(3)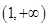 .
.
解析試題分析:(1)兩個函數的圖象關于某條直線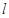 對稱,一般都是設
對稱,一般都是設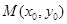 是一個函數圖象上的任一點,求出這個點
是一個函數圖象上的任一點,求出這個點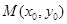 關于直線
關于直線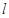 對稱的點
對稱的點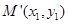 ,而點
,而點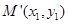 就在第二個函數的圖象上,這樣就把兩個函數建立了聯系;(2)函數
就在第二個函數的圖象上,這樣就把兩個函數建立了聯系;(2)函數 有且只有一個零點,一般是求
有且只有一個零點,一般是求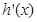 ,通過
,通過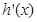 討論函數
討論函數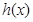 的單調性,最值,從而討論零點的個數,當然本題中由于
的單調性,最值,從而討論零點的個數,當然本題中由于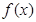 與
與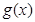 的圖象關于直線
的圖象關于直線 對稱,因此
對稱,因此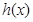 的唯一零點也就是它們的的唯一交點必在直線
的唯一零點也就是它們的的唯一交點必在直線 上,這個交點是函數
上,這個交點是函數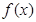 圖象與直線
圖象與直線 的切點,這樣我們可從切線方面來解決問題;(3)考慮
的切點,這樣我們可從切線方面來解決問題;(3)考慮
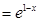
 ,
,
當然要解不等式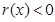 ,還需求
,還需求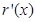 ,討論
,討論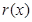 的單調性,極值,從而確定不等式的解集.
的單調性,極值,從而確定不等式的解集.
試題解析:(1)設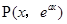 是函數
是函數 圖像上任一點,則它關于直線
圖像上任一點,則它關于直線 對稱的點
對稱的點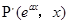 在函數
在函數 的圖像上,
的圖像上,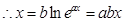 ,
,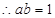 .
.
(2)當 時,函數
時,函數 有且只有一個零點,兩個函數的圖像有且只有一個交點,
有且只有一個零點,兩個函數的圖像有且只有一個交點,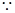 兩個函數關于直線
兩個函數關于直線 對稱,
對稱,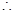 兩個函數圖像的交點就是函數
兩個函數圖像的交點就是函數 ,的圖像與直線
,的圖像與直線 的切點.
的切點.
設切點為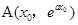 ,
,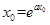
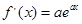 ,
,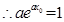 ,
,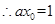 ,
,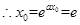 ,
,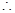 當
當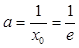 時,函數
時,函數 有且只有一個零點
有且只有一個零點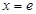 ;
;
(3)當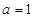 時,設
時,設 
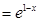
 ,則
,則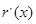
 ,當
,當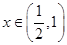 時,
時,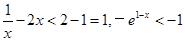 ,
,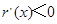 ,
,
當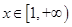 時,
時,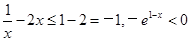 ,
,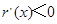 .
.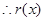 在
在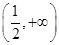 上是減函數.
上是減函數.
又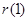 =0,
=0,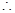 不等式
不等式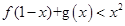 解集是
解集是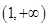 .
.
考點:(1)兩個函數圖象的對稱問題;(2)函數的零點與切線問題;(3)解函數不等式.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
已知函數 的定義域為
的定義域為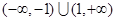 ,對定義域內的任意x,滿足
,對定義域內的任意x,滿足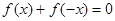 ,當
,當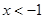 時,
時,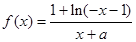 (a為常),且
(a為常),且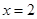 是函數
是函數 的一個極值點,
的一個極值點,
(1)求實數a的值;
(2)如果當 時,不等式
時,不等式 恒成立,求實數m的最大值;
恒成立,求實數m的最大值;
(3)求證: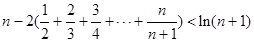
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對于函數 ,若存在實數對(
,若存在實數對( ),使得等式
),使得等式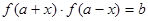 對定義域中的每一個
對定義域中的每一個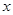 都成立,則稱函數
都成立,則稱函數 是“(
是“( )型函數”.
)型函數”.
(1) 判斷函數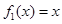 是否為“(
是否為“( )型函數”,并說明理由;
)型函數”,并說明理由;
(2) 若函數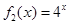 是“(
是“( )型函數”,求出滿足條件的一組實數對
)型函數”,求出滿足條件的一組實數對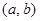 ;
;
(3)已知函數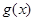 是“(
是“( )型函數”,對應的實數對
)型函數”,對應的實數對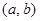 為(1,4).當
為(1,4).當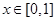 時,
時,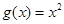
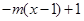
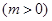 ,若當
,若當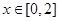 時,都有
時,都有 ,試求
,試求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖所示,一種醫用輸液瓶可以視為兩個圓柱的組合體.開始輸液時,滴管內勻速滴下球狀液體,其中球狀液體的半徑 毫米,滴管內液體忽略不計.
毫米,滴管內液體忽略不計.
(1)如果瓶內的藥液恰好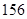 分鐘滴完,問每分鐘應滴下多少滴?
分鐘滴完,問每分鐘應滴下多少滴?
(2)在條件(1)下,設輸液開始后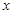 (單位:分鐘),瓶內液面與進氣管的距離為
(單位:分鐘),瓶內液面與進氣管的距離為 (單位:厘米),已知當
(單位:厘米),已知當 時,
時,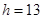 .試將
.試將 表示為
表示為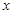 的函數.(注:
的函數.(注: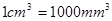 )
)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知二次函數 的導函數的圖像與直線
的導函數的圖像與直線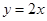 平行,且
平行,且 在
在 處取得極小值
處取得極小值 .設
.設 .
.
(1)若曲線 上的點
上的點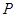 到點
到點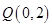 的距離的最小值為
的距離的最小值為 ,求
,求 的值;
的值;
(2)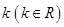 如何取值時,函數
如何取值時,函數 存在零點,并求出零點.
存在零點,并求出零點.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
運貨卡車以每小時 千米的速度勻速行駛130千米
千米的速度勻速行駛130千米
 (單位:千米/小時).假設汽油的價格是每升2元,而汽車每小時耗油
(單位:千米/小時).假設汽油的價格是每升2元,而汽車每小時耗油 升,司機的工資是每小時14元.
升,司機的工資是每小時14元.
(1)求這次行車總費用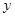 關于
關于 的表達式;
的表達式;
(2)當 為何值時,這次行車的總費用最低,并求出最低費用的值.
為何值時,這次行車的總費用最低,并求出最低費用的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校課外興趣小組的學生為了給學校邊的一口被污染的池塘治污,他們通過實驗后決定在池塘中投放一種能與水中的污染物質發生化學反應的藥劑.已知每投放 個單位的藥劑,它在水中釋放的濃度
個單位的藥劑,它在水中釋放的濃度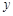 (克/升)隨著時間
(克/升)隨著時間 (天)變化的函數關系式近似為
(天)變化的函數關系式近似為 ,其中
,其中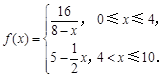 若多次投放,則某一時刻水中的藥劑濃度為各次投放的藥劑在相應時刻所釋放的濃度之和.根據經驗,當水中藥劑的濃度不低于4(克/升)時,它才能起到有效治污的作用.
若多次投放,則某一時刻水中的藥劑濃度為各次投放的藥劑在相應時刻所釋放的濃度之和.根據經驗,當水中藥劑的濃度不低于4(克/升)時,它才能起到有效治污的作用.
(Ⅰ)若一次投放4個單位的藥劑,則有效治污時間可達幾天?
(Ⅱ)若第一次投放2個單位的藥劑,6天后再投放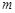 個單位的藥劑,要使接下來的4天中能夠持續有效治污,試求
個單位的藥劑,要使接下來的4天中能夠持續有效治污,試求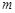 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com