
已知函數 的定義域為
的定義域為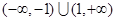 ,對定義域內的任意x,滿足
,對定義域內的任意x,滿足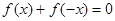 ,當
,當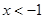 時,
時,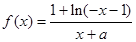 (a為常),且
(a為常),且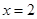 是函數
是函數 的一個極值點,
的一個極值點,
(1)求實數a的值;
(2)如果當 時,不等式
時,不等式 恒成立,求實數m的最大值;
恒成立,求實數m的最大值;
(3)求證: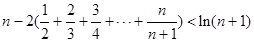
(1)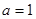 ;(2)2;(3)詳見解析.
;(2)2;(3)詳見解析.
解析試題分析:(1)利用 為奇函數,所以設
為奇函數,所以設 ,利用
,利用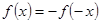 ,求出
,求出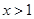 時的
時的 ,然后再求
,然后再求 時的
時的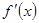 ,再根據
,再根據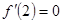 ,求出
,求出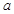 ,驗證所求
,驗證所求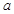 能夠使
能夠使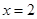 是函數
是函數 的一個極值點;(2)不等式
的一個極值點;(2)不等式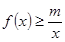 恒成立,轉化為
恒成立,轉化為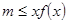 恒成立,設
恒成立,設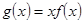 ,即求
,即求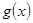 的最小值,求
的最小值,求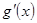
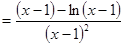 ,再設
,再設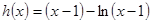 ,易求
,易求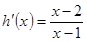 ,當
,當 時,
時,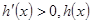 為增函數,
為增函數,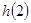 最小,
最小,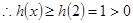 ,即
,即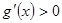 逐步分析
逐步分析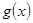 為單調遞增函數,從而求得最小值.(3)通過
為單調遞增函數,從而求得最小值.(3)通過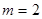 代入(2)式恒成立不等式
代入(2)式恒成立不等式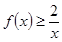 ,變形放縮后得到
,變形放縮后得到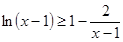 ,為出現(2)要證形式,所以令
,為出現(2)要證形式,所以令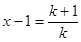 ,則
,則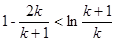 ,然后將k=1,2, n,代入上式,累加,從而得出要證不等式.此題綜合性較強.
,然后將k=1,2, n,代入上式,累加,從而得出要證不等式.此題綜合性較強.
試題解析:(1)由題知對定義域內任意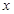 ,
,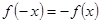 ,
,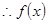 為奇函數,
為奇函數,
當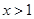 時,
時,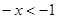 ,
, ,
,
當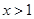 時,
時,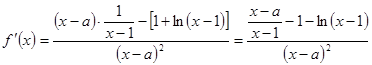
由題知: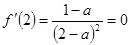 ,解得
,解得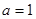 ,經驗證,滿足題意.
,經驗證,滿足題意.
(2)由(1)知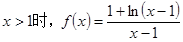
當 時,
時,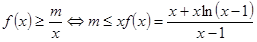 ,令
,令
則 時,
時,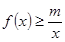 恒成立,轉化為
恒成立,轉化為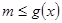 在
在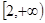 恒成立.
恒成立.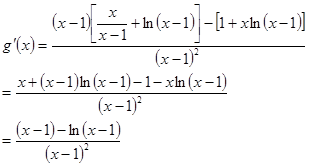
令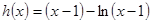 ,
,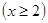 ,則
,則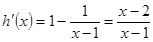 ,
,
當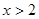 時,
時,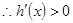 ,
,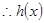 在
在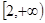 上單調遞增.
上單調遞增.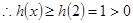
 當
當 時,
時,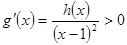 ,
,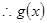 在
在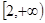 單調遞增.
單調遞增.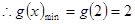
則若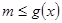 在
在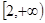 恒成立,則
恒成立,則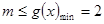
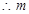 的最大值2.
的最大值2.
(3)由(2)知當 時,有
時,有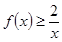 ,即
,即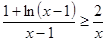
則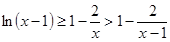
令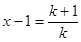 ,則
,則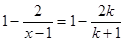


科目:高中數學 來源: 題型:解答題
為了保護環境,發展低碳經濟,某單位在國家科研部門的支持下,進行技術攻關,新上了把二氧化碳處理轉化為一種可利用的化工產品的項目,經測算,該項目月處理成本y(元)與月處理量x(噸)之間的函數關系可近似地表示為
y=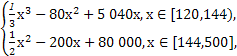
且每處理一噸二氧化碳得到可利用的化工產品價值為200元,若該項目不獲利,國家將給予補償.
(1)當x∈[200,300]時,判斷該項目能否獲利?如果獲利,求出最大利潤;如果不獲利,則國家每月至少需要補貼多少元才能使該項目不虧損?
(2)該項目每月處理量為多少噸時,才能使每噸的平均處理成本最低?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知二次函數f(x)=ax2+bx+1(a>0),F(x)=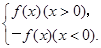 若f(-1)=0,且對任意實數x均有f(x)≥0成立.
若f(-1)=0,且對任意實數x均有f(x)≥0成立.
(1)求F(x)的表達式;
(2)當x∈[-2,2]時,g(x)=f(x)-kx是單調函數,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某單位擬建一個扇環面形狀的花壇(如圖所示),該扇環面是由以點 為圓心的兩個同心圓弧和延長后通過點
為圓心的兩個同心圓弧和延長后通過點 的兩條直線段圍成.按設計要求扇環面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為
的兩條直線段圍成.按設計要求扇環面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為 米,圓心角為
米,圓心角為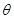 (弧度).
(弧度).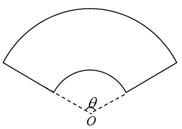
(1)求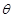 關于
關于 的函數關系式;
的函數關系式;
(2)已知在花壇的邊緣(實線部分)進行裝飾時,直線部分的裝飾費用為4元/米,弧線部分的裝飾費用為9元/米.設花壇的面積與裝飾總費用的比為 ,求
,求 關于
關于 的函數關系式,并求出
的函數關系式,并求出 為何值時,
為何值時, 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某投資公司計劃投資A,B兩種金融產品,根據市場調查與預測,A產品的利潤y1與投資金額x的函數關系為y1=18-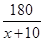 ,B產品的利潤y2與投資金額x的函數關系為y2=
,B產品的利潤y2與投資金額x的函數關系為y2=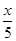 (注:利潤與投資金額單位:萬元).
(注:利潤與投資金額單位:萬元).
(1)該公司已有100萬元資金,并全部投入A,B兩種產品中,其中x萬元資金投入A產品,試把A,B兩種產品利潤總和表示為x的函數,并寫出定義域;
(2)在(1)的條件下,試問:怎樣分配這100萬元資金,才能使公司獲得最大利潤?其最大利潤為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
我國加入WTO后,根據達成的協議,若干年內某產品關稅與市場供應量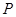 的關系允許近似的滿足:
的關系允許近似的滿足: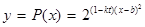 (其中
(其中 為關稅的稅率,且
為關稅的稅率,且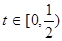 ,
, 為市場價格,
為市場價格,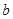 、
、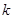 為正常數),當
為正常數),當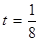 時的市場供應量曲線如圖:
時的市場供應量曲線如圖: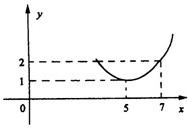
(1)根據圖象求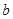 、
、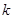 的值;
的值;
(2)若市場需求量為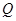 ,它近似滿足
,它近似滿足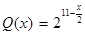 .當
.當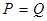 時的市場價格稱為市場平衡價格.為使市場平衡價格控制在不低于9元,求稅率
時的市場價格稱為市場平衡價格.為使市場平衡價格控制在不低于9元,求稅率 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com