Question

點P是雙曲線

y2

9

-

x2

16

=1的上支上的一點，F₁，F₂分別為雙曲線的上、下焦點，則△PF₁F₂的內切圓圓心M的坐標一定適合的方程是（　　）

A．y=-3

B．y=3

C．x²+y²=5

D．y=3x²-2

Answer 1

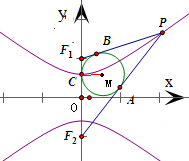
分析：根據題意，設△PF₁F₂的內切圓分別與PF₁、PF₂切于點A、B，與F₁F₂切于點C，由圓的切線長定理得|PA|=|PB|，|F₁B|=|F₁C|且|F₂A|=|F₂C|，結合雙曲線的定義算出在實軸上的切點C坐標為（0，3）．因為CM⊥y軸，所以得到CM所在直線方程為y=3，得到本題答案．

解答：解：∵雙曲線的方程為

y2

9

-

x2

16

=1，
∴a²=9，b²=16，得c=

a2+b2

=5
設△PF₁F₂的內切圓分別與PF₁、PF₂切于點A、B，與F₁F₂切于點C，
則|PA|=|PB|，|F₁B|=|F₁C|，|F₂A|=|F₂C|，
又∵點P在雙曲線上支上，
∴|PF₂|-|PF₁|=2a=6，
即（|F₂A|+|PA|）-（|F₁B|+|PB|）=6，化簡得|F₂A|-|F₁B|=6，
即|F₂C|-|F₁C|=6，而|F₁C|+|F₂C|=2c=10，
設C點坐標為（0，λ），由|F₂C|-|F₁C|=6可得（λ+5）-（5-λ）=6
解之得λ=3，得C的坐標為（0，3）
∵圓M與F₁F₂切于點C，
∴CM⊥y軸，可得CM所在直線方程為y=3

點評：本題給出雙曲線的焦點三角形，求三角形的內切圓圓心滿足的條件，著重考查了雙曲線的定義與簡單幾何性質、三角形的內切圓、直線與圓的位置關系等知識，屬于中檔題．