Question

設數列{a_n}的首項不為零，前n項和為S_n，且對任意的r，tN^*，都有．
（1）求數列{a_n}的通項公式（用a₁表示）；
（2）設a₁=1，b₁=3，，求證：數列為等比數列；
（3）在（2）的條件下，求．

Answer 1

（1）;（2）詳見解析;（3）．

解析試題分析：（1）根據題中所給數列遞推關系的特征：，有且只有前n項和的比值，而題中又要求以a₁表示，即可想到令，，得到，這樣問題即可轉化為由求的問題，注意要分三步啊; （2）由（1）中所求的表達式，并已知a₁=1，即可確定出的通項公式和前n項和公式，再運用條件，不難求出關系：，結合所證數列的特征和等比數列的定義，可得，即可得證;（3）由在（2）的條件下，即可得出的通項公式：化簡得，觀察其特點和所求目標，不難想到求出：，運用代數知識化簡得：，這樣就可聯想到數列求和中的裂項相消的方法，可得：．
試題解析：（1）因為，令，，則，得，即． 2分
當時，，且當時，此式也成立．
故數列{a_n}的通項公式為．                                   5分
（2）當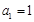時，由（1）知，S_n＝n²．
依題意，時，，                                         7分
于是，且，
故數列是首項為1，公比為2的等比數列．                          10分
（3）由（2）得，所以．                  12分
于是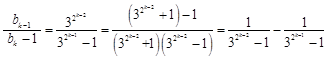．                   15分
所以．                      16分
考點：1.遞推關系的處理;2.等比數列的定義;3.數列求和的應用