Question

在△ABC中，角所對的邊分別為，且∥
（Ⅰ）求的值
（Ⅱ）求三角函數式的取值范圍

Answer 1

(Ⅰ) ；（Ⅱ）三角函數式的取值范圍為（-1，]．

解析試題分析：（I）求的值，可考慮利用正弦定理，也可利用面積公式，但本題由已知且∥，可根據向量平行的充要條件列式：，結合正弦定理與正弦的誘導公式，兩角和的正弦公式化簡整理，化簡可得，可得，從而得到的值；（II）求三角函數式的取值范圍，將三角函數式用二倍角的余弦公式結合“切化弦”，化簡整理得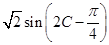，再根據算出的范圍，得到的取值范圍，最終得到原三角函數式的取值范圍．
試題解析：(Ⅰ)∵且∥，∴
由正弦定理得2sinAcosC=2sinB-sinC， 又sinB=sin(A+C)=sinAcosC+cosAsinC，∴sinC=cosAsinC
∵sinC≠0   ∴cosA=，
又∵0<A<p,  ∴A=，    ∴
(Ⅱ)原式=+1=1-=1-2cos²C+2sinCcosC=sin2C-cos2C=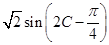
∵0<C<p   ∴<2C-<， ∴< sin(2C-)≤1
∴-1<sin(2C-)≤，  即三角函數式的取值范圍為（-1，]
考點：三角函數中的恒等變換應用；平面向量共線（平行）的坐標表示．