設函數f(x)＝ax2＋(b－2)x＋3(a≠0)，若不等式f(x)＞0的解集為(－1,3)．
(1)求a，b的值；
(2)若函數f(x)在x∈[m,1]上的最小值為1，求實數m的值．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：解答題
某房地產開發商投資81萬元建一座寫字樓，第一年需維護費用為1萬元，以后每年增加2萬元，若把寫字樓出租，每年收入租金30萬元．
（1）開發商最早在第幾年獲取純利潤？
（2）若干年后開發商為了投資其它項目，有兩種處理方案：①純利潤最大時，以10萬元出售該樓；②年平均利潤最大時以46萬元出售該樓．問哪種方案更優？并說明理由？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知函數f(x)＝ax2－2ax＋2＋b(a≠0)，若f(x)在區間[2,3]上有最大值5，最小值2.
(1)求a，b的值；
(2)若b<1，g(x)＝f(x)－mx在[2,4]上單調，求m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某食品公司為了解某種新品種食品的市場需求,進行了20天的測試,人為地調控每天產品的單價P(元/件)：前10天每天單價呈直線下降趨勢(第10天免費贈送品嘗),后10天呈直線上升,其中4天的單價記錄如表：
| 時間(將第x天記為x)x | 1 | 10 | 11 | 18 |
| 單價(元/件)P | 9 | 0 | 1 | 8 |
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（2011•湖北）提高過江大橋的車輛通行能力可改善整個城市的交通狀況，在一般情況下，大橋上的車流速度v（單位：千米/小時）是車流密度x（單位：輛/千米）的函數，當橋上的車流密度達到200輛/千米時，造成堵塞，此時車流速度為0；當車流密度不超過20輛/千米時，車流速度為60千米/小時，研究表明：當20≤x≤200時，車流速度v是車流密度x的一次函數．
（1）當0≤x≤200時，求函數v（x）的表達式；
（2）當車流密度x為多大時，車流量（單位時間內通過橋上某觀測點的車輛數，單位：輛/小時）f（x）=x•v（x）可以達到最大，并求出最大值．（精確到1輛/小時）．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
如圖，某小區有一邊長為2（單位：百米）的正方形地塊OABC，其中OAE是一個游泳池，計劃在地塊OABC內修一條與池邊AE相切的直路
（寬度不計），切點為M，并把該地塊分為兩部分．現以點O為坐標原點，以線段OC所在直線為x軸，建立平面直角坐標系，若池邊AE滿足函數
）的圖象，且點M到邊OA距離為
．
（1）當
時，求直路所在的直線方程；
（2）當t為何值時，地塊OABC在直路不含泳池那側的面積取到最大，最大值是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
提高過江大橋的車輛通行能力可改善整個城市的交通狀況．在一般情況下，大橋上的車流速度
（單位：千米/小時）是車流密度
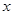（單位：輛/千米）的函數．當橋上的車流密度達到200輛/千米時，造成堵塞，此時車流速度為0；當車流密度不超過20輛/千米時，車流速度為60千米/小時．研究表明：當
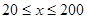時，車流速度是車流密度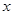的一次函數．
（1）當
時，求函數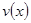
的表達式；
（2）當車流密度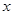為多大時，車流量（單位時間內通過橋上某觀測點的車輛數，單位：輛/小時）
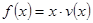可以達到最大，并求出最大值．（精確到1輛/小時）
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
我國遼東半島普蘭附近的泥炭層中，發掘出的古蓮子，至今大部分還能發芽開花，這些古蓮子是多少年以前的遺物呢？要測定古物的年代，可用放射性碳法．在動植物的體內都含有微量的放射性14C，動植物死亡后，停止了新陳代謝，14C不再產生，且原有的14C會自動衰變，經過5570年(叫做14C的半衰期)，它的殘余量只有原始量的一半，經過科學家測定知道，若14C的原始含量為a，則經過t年后的殘余量a′(與a之間滿足a′＝a·e－kt)．現測得出土的古蓮子中14C殘余量占原量的87.9%，試推算古蓮子的生活年代．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的二次項系數為
，且不等式
的解集為（1，3）．
有兩個相等實數根，求