
提高過江大橋的車輛通行能力可改善整個城市的交通狀況.在一般情況下,大橋上的車流速度 (單位:千米/小時)是車流密度
(單位:千米/小時)是車流密度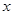 (單位:輛/千米)的函數.當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時.研究表明:當
(單位:輛/千米)的函數.當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時.研究表明:當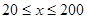 時,車流速度
時,車流速度 是車流密度
是車流密度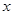 的一次函數.
的一次函數.
(1)當 時,求函數
時,求函數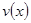 的表達式;
的表達式;
(2)當車流密度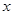 為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)
為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)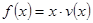 可以達到最大,并求出最大值.(精確到1輛/小時)
可以達到最大,并求出最大值.(精確到1輛/小時)
(1) ,(2)100輛/千米,3333輛/千米
,(2)100輛/千米,3333輛/千米
解析試題分析:(1)解實際問題,關鍵在于正確理解題意.本題為求函數關系式,是一個分段函數. 當車流密度不超過20輛/千米時,是一個常函數,當車流密度滿足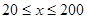 時,車流速度
時,車流速度 是車流密度
是車流密度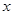 的一次函數,這需要利用待定系數法求解,所以
的一次函數,這需要利用待定系數法求解,所以 ,(2)求分段函數最值,需先分段求最值,再比較大小得原函數最值. 當
,(2)求分段函數最值,需先分段求最值,再比較大小得原函數最值. 當 時,
時, 為增函數,故當
為增函數,故當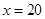 時,其最大值為
時,其最大值為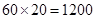 ;當
;當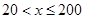 時,
時,  時,
時, 取得最大值
取得最大值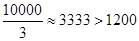 ,所以當車流密度為100輛/千米時,車流量可以達到最大,最大值約為3333輛/小時.
,所以當車流密度為100輛/千米時,車流量可以達到最大,最大值約為3333輛/小時.
試題解析:(1)
(2)依題意并由(Ⅰ)可得
當 時,
時, 為增函數,故當
為增函數,故當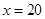 時,其最大值為
時,其最大值為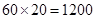 ;
;
當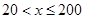 時,
時,  時,
時, 在取得最大值
在取得最大值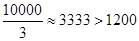 .
.
即當車流密度為100輛/千米時,車流量可以達到最大,最大值約為3333輛/小時.
考點:分段函數解析式及其最值


科目:高中數學 來源: 題型:解答題
設函數f(x)=ax2+(b-2)x+3(a≠0),若不等式f(x)>0的解集為(-1,3).
(1)求a,b的值;
(2)若函數f(x)在x∈[m,1]上的最小值為1,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
定義在[﹣1,1]上的奇函數f(x)滿足f(1)=2,且當a,b∈[﹣1,1],a+b≠0時,有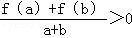 .
.
(1)試問函數f(x)的圖象上是否存在兩個不同的點A,B,使直線AB恰好與y軸垂直,若存在,求出A,B兩點的坐標;若不存在,請說明理由并加以證明.
(2)若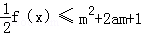 對所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求實數m的取值范圍.
對所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某商品每件成本9元,售價為30元,每星期賣出144件. 如果降低價格,銷售量可以增加,且每星期多賣出的商品件數與商品單價的降低值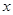 (單位:元,
(單位:元, )的平方成正比.
)的平方成正比.
已知商品單價降低2元時,一星期多賣出8件.
(1)將一個星期的商品銷售利潤表示成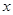 的函數;
的函數;
(2)如何定價才能使一個星期的商品銷售利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲同學家到乙同學家的途中有一公園,甲從家到公園的距離與乙從家到公園的距離都是2 km,甲10時出發前往乙家.如圖所示,表示甲從家出發到達乙家為止經過的路程y(km)與時間x(分)的關系.試寫出y=f(x)的函數解析式.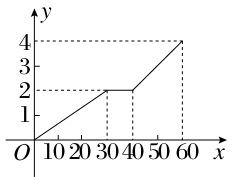
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com