中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

橢圓E的中心在原點O，焦點在軸上，其離心率, 過點C（－1,0）的直線與橢圓E相交于A、B兩點，且滿足點C分向量的比為2.

（1）用直線的斜率k ( k≠0 ) 表示△OAB的面積；（2）當△OAB的面積最大時，求橢圓E的方程。

解：（1）設橢圓E的方程為( a＞b＞0 )，由e =

∴a2=3b2   故橢圓方程x2 + 3y2 = 3b2

設A(x1,y1)、B(x2,y2),由于點C（－1，0）分向量的比為2，

①

②
 
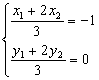∴             即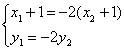

由消去y整理并化簡得    (3k2+1)x2+6k2x+3k2－3b2=0

由直線l與橢圓E相交于A（x1,y1）, B(x2,y2)兩點得：

③

④

⑤
 
  

而S△OAB  ⑤

由①③得:x2+1=－，代入⑤得：S△OAB  =

（2）因S△OAB=,

當且僅當S△OAB取得最大值

此時 x1 + x2 =－1, 又∵  =－1    ∴x1=1,x2 =－2

將x1,x2及k2 = 代入④得3b2 = 5 ∴橢圓方程x2 + 3y2 = 5

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

橢圓E的中心在原點O，焦點在x軸上，離心率e=
2
3
，過點C（-1，0）的直線l交橢圓于A、B兩點，且滿足：
CA
=λ
BC
（λ≥2）．
（1）若λ為常數，試用直線l的斜率k（k≠0）表示三角形OAB的面積；
（2）若λ為常數，當三角形OAB的面積取得最大值時，求橢圓E的方程；
（3）若λ變化，且λ=k2+1，試問：實數λ和直線l的斜率k（k∈R）分別為何值時，橢圓E的短半軸長取得最大值？并求出此時的橢圓方程．

查看答案和解析>>

科目：高中數學 來源：2010-2011學年黑龍江省雞西市高三上學期期末理科數學卷 題型：解答題

橢圓E的中心在原點O，焦點在x軸上，離心率e=，過點C(-1，0)的直線交橢圓于A，B兩點，且滿足，為常數。

（1）當直線的斜率k=1且時，求三角形OAB的面積.

（2）當三角形OAB的面積取得最大值時，求橢圓E的方程.

 

查看答案和解析>>

科目：高中數學 來源： 題型：

（本題滿分12分）橢圓E的中心在原點O，焦點在x軸上，離心率e=，過點C（-1，0）的直線交橢圓于A，B兩點，且滿足，為常數。

       （1）當直線的斜率k=1且時，求三角形OAB的面積．

       （2）當三角形OAB的面積取得最大值時，求橢圓E的方程．

查看答案和解析>>

科目：高中數學 來源：2010年河南省鄭州47中高考模擬數學試卷（解析版） 題型：解答題

橢圓E的中心在原點O，焦點在x軸上，離心率，過點C（-1，0）的直線l交橢圓于A、B兩點，且滿足：（λ≥2）．
（1）若λ為常數，試用直線l的斜率k（k≠0）表示三角形OAB的面積；
（2）若λ為常數，當三角形OAB的面積取得最大值時，求橢圓E的方程；
（3）若λ變化，且λ=k2+1，試問：實數λ和直線l的斜率k（k∈R）分別為何值時，橢圓E的短半軸長取得最大值？并求出此時的橢圓方程．

查看答案和解析>>

同步練習冊答案