
��֪�����c(di��n)C(t, )(t��R,t��0)��A�ĵĈA�c
)(t��R,t��0)��A�ĵĈA�c �S�����c(di��n)O,A���cy�S�����c(di��n)O,B������O��ԭ�c(di��n)
�S�����c(di��n)O,A���cy�S�����c(di��n)O,B������O��ԭ�c(di��n)
��1�����C����OAB����e�鶨ֵ��
��2���O(sh��)ֱ��y=�C2x+4�c�AC�����c(di��n)M,N����OM=ON����AC�ķ���
(1)����������(2)
����ԇ�}������(1)��?y��n)�Ҫ�C��OAB����e�鶨ֵ���P(gu��n)�I��Ҫ���A,B���c(di��n)������(bi��o) ����(j��)�A�İ돽�� ��
�� ���Կ��Ԍ����AC�ķ��� �Ķ��քe��
���Կ��Ԍ����AC�ķ��� �Ķ��քe�� �������A,B���c(di��n)������(bi��o) �ٸ���(j��)
�������A,B���c(di��n)������(bi��o) �ٸ���(j��) �ͼ����C�ýY(ji��)Փ
�ͼ����C�ýY(ji��)Փ
(2)��?y��n)�ֱ��y=�C2x+4�c�AC�����c(di��n)M,N����OM="ON" ����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/97/5/1iqs14.png" style="vertical-align:middle;" />���Կɵ� ��ֱ��
��ֱ�� ��б�ʼ������ֱ��
��б�ʼ������ֱ�� ��б�ʣ��Ķ��õ�ֱ��
��б�ʣ��Ķ��õ�ֱ�� �ķ��̣��ڴ���C (t,
�ķ��̣��ڴ���C (t, ) �������
) ������� ��ֵ���ٸ���(j��)
��ֵ���ٸ���(j��) ��ֵ�Д�ֱ���c�A���P(gu��n)ϵ �Ķ��_���A�ķ���
��ֵ�Д�ֱ���c�A���P(gu��n)ϵ �Ķ��_���A�ķ���
ԇ�}��������1����?y��n)�AC�^ԭ�c(di��n)O��
�O(sh��)�A �ķ�����
�ķ�����  ��
�� ��
�� ����
����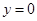 ��
�� ����
���� ,��
,�� ����e�鶨ֵ
����e�鶨ֵ
��2����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/a9/0/1tbj53.png" style="vertical-align:middle;" />��ֱƽ�־��� ��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/e2/c/1tijj2.png" style="vertical-align:middle;" />,����ֱ��
��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/e2/c/1tijj2.png" style="vertical-align:middle;" />,����ֱ�� �ķ�����
�ķ����� ����
���� �����
����� ��
�� ��(d��ng)
��(d��ng) �r���A��
�r���A�� ������(bi��o)��
������(bi��o)��
�˕r ��ֱ��
��ֱ�� �ľ��x
�ľ��x ��
��
�A �cֱ��
�cֱ�� �ཻ�ڃ��c(di��n) 10��
�ཻ�ڃ��c(di��n) 10��
��(d��ng) �r���A��
�r���A�� ������(bi��o)��
������(bi��o)�� ��
�� ��
��
�˕r ��ֱ��
��ֱ�� �ľ��x
�ľ��x
�A �cֱ��
�cֱ�� ���ཻ��
���ཻ�� �������}����ȥ 11��
�������}����ȥ 11�� �A
�A �ķ��̞�
�ķ��̞� 13��
13��
���c(di��n)��1 �A�ķ��� 2 ֱ���c�A�ķ��� 3 �A�Č��Q��



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�AM�^���c(di��n)A(1����1)��B(��1��1)���҈A��M��x��y��2��0�ϣ�
(1)��AM�ķ��̣�
(2)�O(sh��)P��ֱ��3x��4y��8��0�ϵĄ��c(di��n)��PA�䡢PB���LjAM�ăɗl�о���A�䡢B������c(di��n)������߅��PA��MB����e����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�A �ķ��̞�
�ķ��̞� ,�c(di��n)
,�c(di��n) ������(bi��o)ԭ�c(di��n).ֱ��
������(bi��o)ԭ�c(di��n).ֱ��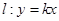 �c�A
�c�A ����
����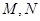 ���c(di��n).
���c(di��n).
��1���� ��ȡֵ����;
��ȡֵ����;
��2���^ ���A���ң�����С���L��
���A���ң�����С���L��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�A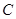 ��(j��ng)�^����(bi��o)ԭ�c(di��n)
��(j��ng)�^����(bi��o)ԭ�c(di��n) ���c(di��n)
���c(di��n)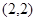 ���҈A����
���҈A���� �S��.
�S��.
��1����A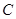 �ķ��̣�
�ķ��̣�
��2���O(sh��)ֱ�� ��(j��ng)�^�c(di��n)
��(j��ng)�^�c(di��n) ����
���� �c�A
�c�A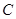 �ཻ�������L��
�ཻ�������L�� ����ֱ��
����ֱ�� �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��돽�� ���A����ֱ��
���A����ֱ�� ��
��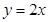 �ϣ��ұ�ֱ��
�ϣ��ұ�ֱ�� ��
�� �����ҵ��L��
�����ҵ��L�� �ĈA�ķ���.
�ĈA�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D����֪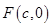 �ǙE�A
�ǙE�A ���ҽ��c(di��n)���A
���ҽ��c(di��n)���A �c
�c �S����
�S���� ���c(di��n)������
���c(di��n)������ �ǙE�A
�ǙE�A �����c(di��n).
�����c(di��n).
��1����E�A ���x���ʣ�
���x���ʣ�
��2���O(sh��)�A �c
�c �S�������S�Ľ��c(di��n)��
�S�������S�Ľ��c(di��n)�� ���c(di��n)
���c(di��n) ���c(di��n)
���c(di��n) �P(gu��n)��
�P(gu��n)�� �S�Č��Q�c(di��n)��ԇ�Д�ֱ��
�S�Č��Q�c(di��n)��ԇ�Д�ֱ�� �c�A
�c�A ��λ���P(gu��n)ϵ��
��λ���P(gu��n)ϵ��
��3���O(sh��)ֱ�� �c�A
�c�A ������һ�c(di��n)
������һ�c(di��n) ����
����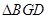 ����e��
����e�� ����E�A
����E�A ��(bi��o)��(zh��n)����.
��(bi��o)��(zh��n)����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
(1)��ֱ�� �P(gu��n)��ֱ��
�P(gu��n)��ֱ��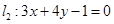 ,���Q��ֱ�����̣�
,���Q��ֱ�����̣�
(2)��֪��(sh��)��(sh��)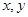 �M��
�M�� ����
���� ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��ƽ��ֱ������(bi��o)ϵ �У���֪�A
�У���֪�A ��
�� ��ֱ��
��ֱ�� ��
�� ��
�� ��
�� ��һ���c(di��n)��
��һ���c(di��n)�� ��
�� ��A
��A �c
�c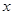 �S�ăɂ����c(di��n)��ֱ��
�S�ăɂ����c(di��n)��ֱ�� ��
�� �c�A
�c�A ����һ�����c(di��n)�քe��
����һ�����c(di��n)�քe�� ��
��
��1���� �c(di��n)������(bi��o)��(4��2)����ֱ��
�c(di��n)������(bi��o)��(4��2)����ֱ�� ���̣�
���̣�
��2�����Cֱ�� �^���c(di��n)��������˶��c(di��n)������(bi��o)��
�^���c(di��n)��������˶��c(di��n)������(bi��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�c(di��n) �LjA
�LjA �ϵ��c(di��n)
�ϵ��c(di��n)
��1���� ��ȡֵ����;
��ȡֵ����;
��2���� ���������(sh��)��(sh��)
���������(sh��)��(sh��) ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com