
已知等差數列 的前四項和為10,且
的前四項和為10,且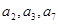 成等比數列
成等比數列
(1)求通項公式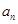
(2)設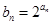 ,求數列
,求數列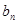 的前
的前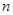 項和
項和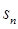 。
。
⑴ ;⑵
;⑵ 或
或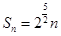 。
。
解析試題分析:(1)利用等差數列的通項公式分別表示出前四項和與a2,a3,a7等比數列關系組成方程組求得a1和d,最后根據等差數列的通項公式求得an.
(2)把(1)中求得的an代入bn=2an中,可知數列{bn}為等比數列,進而根據等比數列的求和公式求得答案.
⑴由題意知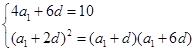

所以 …………6分
…………6分
⑵當 時,數列
時,數列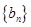 是首項為
是首項為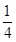 、公比為8的等比數列
、公比為8的等比數列
所以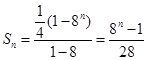 …………9分
…………9分
當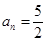 時,
時,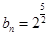 所以
所以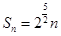
綜上,所以 或
或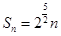 …………12分
…………12分
考點:本題主要考查了等差數列和等比數列的性質.考查了對數列通項公式和求和公式等基本知識的靈活運用.
點評:解決該試題的關鍵是利用等差數列的通項公式和等比數列的通項公式來求解通項公式,進而結合錯位相減法得到求和。


 走進文言文系列答案
走進文言文系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知等差數列{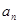 }的前項和為
}的前項和為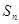 ,且
,且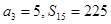 。數列
。數列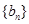 為等比數列,且首項
為等比數列,且首項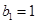 ,
,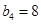 .
.
(1)求數列 ,
,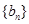 的通項公式;
的通項公式;
(2)若數列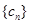 滿足
滿足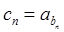 ,求數列
,求數列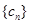 的前
的前 項和為
項和為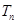 ;
;
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知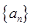 是首項為
是首項為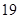 ,公差為
,公差為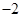 的等差數列,
的等差數列,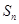 為
為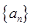 的前
的前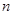 項和.
項和.
(I)求通項 及
及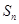 ;
;
(II)設 是首項為1,公比為3的等比數列,求數列
是首項為1,公比為3的等比數列,求數列 的通項公式及其前
的通項公式及其前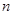 項和
項和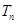 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分14分)
已知函數 的圖像經過點
的圖像經過點 .
.
(1)求該函數的解析式;
(2)數列 中,若
中,若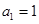 ,
, 為數列
為數列 的前
的前 項和,且滿足
項和,且滿足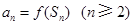 ,
,
證明數列 成等差數列,并求數列
成等差數列,并求數列 的通項公式;
的通項公式;
(3)另有一新數列 ,若將數列
,若將數列 中的所有項按每一行比上一行多一項的規則排成
中的所有項按每一行比上一行多一項的規則排成
如下數表:
 |
  |
   |
    |
 構成的數列即為數列
構成的數列即為數列 ,上表中,若從第三行起,第一行中的數按從左到右的順序均構成等比數列,且公比為同一個正數.當
,上表中,若從第三行起,第一行中的數按從左到右的順序均構成等比數列,且公比為同一個正數.當 時,求上表中第
時,求上表中第 行所有項的和.
行所有項的和.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com