中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

（本小題滿分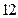分）某學校高三年級有學生1000名，經調查研究,其中750名同學經常參加體育鍛煉（稱為A類同學），另外250名同學不經常參加體育鍛煉(稱為B類同學），現用分層抽樣方法（按A類、B類分二層）從該年級的學生中共抽查100名同學.
(Ⅰ)求甲、乙兩同學都被抽到的概率，其中甲為A類同學，乙為B類同學；
(Ⅱ) 測得該年級所抽查的100名同學身高(單位：厘米) 頻率分布直方圖如右圖：
(ⅰ) 統計方法中，同一組數據常用該組區間的中點值（例如區間的中點值為165）作為代表．據此，計算這100名學生身高數據的期望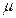及標準差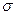(精確到0.1)；
(ⅱ) 若總體服從正態分布,以樣本估計總體,據此,估計該年級身高在范圍中的學生的人數．
(Ⅲ) 如果以身高達170cm作為達標的標準，對抽取的100名學生,得到下列聯表:
體育鍛煉與身高達標2×2列聯表

 
身高達標
身高不達標
總計
積極參加體育鍛煉
40
 
 
不積極參加體育鍛煉
 
15
 
總計
 
 
100
(ⅰ)完成上表；
(ⅱ)請問有多大的把握認為體育鍛煉與身高達標有關系?
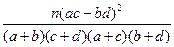參考公式:K=,參考數據:
P(Kk)
0.40
0.25
0.15
0.10
0.05
0.025
k
0.708
1.323
2.072
2.706
3.841
5.024

（1）1/100（2）=170,（3）（）

解析

練習冊系列答案
相關習題

科目：高中數學 來源：2011屆湖南省長沙市第一中學高三第四次月考理科數學試卷 題型：解答題

（本小題滿分13分）某企業的產品以往專銷歐美市場，在全球金融風暴的影響下，歐美市場的銷量受到嚴重影響，該企業在政府的大力扶助下積極開拓國內市場，并基本形成了市場規模；自2009年9月以來的第n個月（2009年9月為第一個月）產品的內銷量、出口量和銷售總量（銷售總量=內銷量與出口量的和）分別為bn、cn和an(單位：萬件)，依據銷售統計數據發現形成如下營銷趨勢：bn + 1 =" a" an，cn + 1 =" an" + b an2 （其中a、b為常數），已知a1 = 1萬件，a2 = 1.5萬件，a3 = 1.875萬件．
（1）求a，b的值，并寫出an + 1與an滿足的關系式；
（2）試用你所學的數學知識論證銷售總量逐月遞增且控制在2萬件內；
（3）試求從2009年9月份以來的第n個月的銷售總量an關于n的表達式．

查看答案和解析>>

科目：高中數學 來源：2012-2013學年遼寧省高三第五次模擬理數試卷（解析版） 題型：解答題

（本小題滿分12分）

某大學高等數學老師上學期分別采用了兩種不同的教學方式對甲、乙兩個大一新生班進行教改試驗（兩個班人數均為60人，入學數學平均分數和優秀率都相同；勤奮程度和自覺性都一樣）。現隨機抽取甲、乙兩班各20名同學的上學期數學期末考試成績，得到莖葉圖如下：

（Ⅰ）依莖葉圖判斷哪個班的平均分高？

（Ⅱ）從乙班這20名同學中隨機抽取兩名高等數學成績不得低于85分的同學，求成績為90分的同學被抽中的概率；

（Ⅲ）學校規定：成績不低于85分的為優秀，請填寫下面的列聯表，并判斷“能否在犯錯誤的概率不超過0.025的前提下認為成績優秀與教學方式有關？”

 

甲班

乙班

合計

優秀

 

 

 

不優秀

 

 

 

合計

 

 

 

下面臨界值表僅供參考：

0.15

0.10

0.05

0.025

0.010

0.005

0.001

2.072

2.706

3.841

5.024

6.635

7.879

10.828

（參考公式：其中） 

（Ⅳ）從乙班高等數學成績不低于85分的同學中抽取2人，成績不低于90分的同學得獎金100元，否則得獎金50元，記為這2人所得的總獎金，求的分布列和數學期望。

 

查看答案和解析>>

科目：高中數學 來源：2014屆江西省高二第一次月考理科數學試卷（解析版） 題型：解答題

（本小題滿分１２分）某企業員工500人參加“學雷鋒”志愿活動，按年齡分組：第1組[25，30)，第2組[30，35)，第3組[35，40)，第4組[40，45)，第5組[45，50]，得到的頻率分布直方圖如右圖所示．

(1)下表是年齡的頻數分布表，求正整數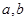的值；

區間

[25，30)

[30，35)

[35，40)

[40，45)

[45，50]

人數

50

50

150

 

 

 

 

 

(2)現在要從年齡較小的第1,2,3組中用分層抽樣的方法抽取6人，年齡在第1,2,3組的人數分別是多少？

(3)在(2)的前提下，從這6人中隨機抽取2人參加社區宣傳交流活動，求至少有1人年齡在第3組的概率．

 

查看答案和解析>>

科目：高中數學 來源：2011-2012學年山西省太原市高三2月月考文科數學 題型：解答題

（本小題滿分12分）

為了解某班學生喜愛打籃球是否與性別有關，對本班50人進行了問卷調查得到了如下的列聯表：

 

喜愛打籃球

不喜愛打籃球

合計

男生

 

5

 

女生

10

 

[來源:學|科|網]

合計

 

 

50[]

已知在全部50人中隨機抽取1人抽到喜愛打籃球的學生的概率為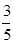

（1）請將上面的列聯表補充完整

（2）是否有99.5％的把握認為喜愛打籃球與性別有關？說明你的理由；

（3）已知喜愛打籃球的10位女生中，還喜歡打羽毛球，

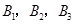
還喜歡打乒乓球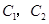，還喜歡踢足球，現在從喜歡打羽毛球、喜歡打乒乓球、

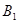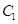喜歡踢足球的8位女生中各選出1名進行其他方面的調查，求和不全被選

中的概率．

下面的臨界值表供參考：

0.15

0.10

0.05

0.025

0.010

0.005

0.001

2.072

2.706

3.841

5.024

6.635

7.879

10.828

 

查看答案和解析>>

科目：高中數學 來源：北京朝陽區09-10學年高一第二學期期末考試數學試題 題型：解答題

（本小題滿分14分）

某校高一年級要從3名男生，，和2名女生，中任選3名代表參加學校的演講比賽.學

科網          （1）求男生被選中的概率；

  （2）求男生和女生至少一人被選中的概率.

 

查看答案和解析>>

同步練習冊答案