
已知定義在 上的函數
上的函數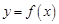 是偶函數,且
是偶函數,且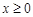 時,
時,
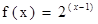 .
.
(1)當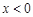 時,求
時,求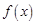 解析式;
解析式;
(2)當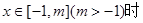 ,求
,求 取值的集合.
取值的集合.
(3)當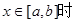 ,函數的值域為
,函數的值域為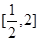 ,求
,求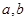 滿足的條件。
滿足的條件。
、解:(1)當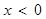 時
時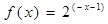
(2)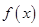 取值的集合為
取值的集合為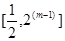
綜上:當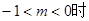 ,
,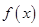 取值的集合為
取值的集合為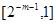
當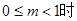 ,
,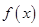 取值的集合為
取值的集合為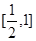
當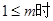 ,
,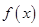 取值的集合為
取值的集合為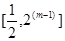
(3)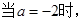
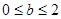
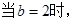
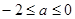
【解析】本試題主要是考查了函數的解析式和函數的值域以及函數的奇偶性的綜合運用。
(1)利用奇偶性得到對稱區間的解析式。
(2)需要對參數m討論可知得到二次函數的值域。
(3)當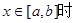 ,函數的值域為
,函數的值域為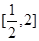 ,
,
由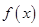 的單調性和對稱性知,
的單調性和對稱性知,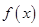 的最小值為
的最小值為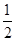 ,從而得到a,b的關系式。
,從而得到a,b的關系式。
解:(1)函數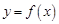 是偶函數,
是偶函數,

當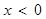 時,
時,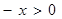
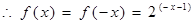
當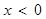 時
時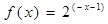
(2)當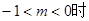 ,
,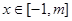 ,
,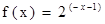 為減函數
為減函數
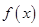 取值的集合為
取值的集合為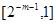
當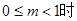 ,
,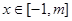 ,
,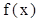 在區間
在區間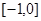 為減函數,在區間
為減函數,在區間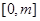 為增函數
為增函數
且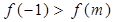 ,
,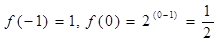
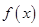 取值的集合為
取值的集合為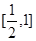
當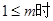 ,
,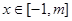 ,
,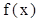 在區間
在區間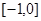 為減函數,在區間
為減函數,在區間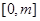 為增函數
為增函數
且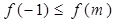 ,
,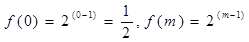
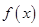 取值的集合為
取值的集合為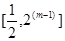
綜上:當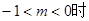 ,
,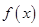 取值的集合為
取值的集合為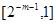
當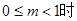 ,
,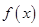 取值的集合為
取值的集合為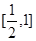
當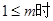 ,
,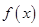 取值的集合為
取值的集合為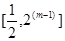
(3)當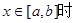 ,函數的值域為
,函數的值域為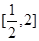 ,
,
由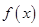 的單調性和對稱性知,
的單調性和對稱性知,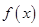 的最小值為
的最小值為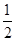 ,
,
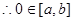 ,
,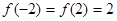
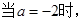
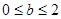
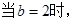
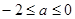


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:2012-2013學年貴州黔東南州高三第二次模擬(5月)考試理科數學試卷(解析版) 題型:選擇題
已知定義在 上的函數
上的函數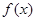 是周期為
是周期為 的偶函數,當
的偶函數,當 時,
時, ,如果直線
,如果直線 與曲線
與曲線 恰有兩個交點,則實數
恰有兩個交點,則實數 的值是( )
的值是( )
A.
B.
C. 或
或
D. 或
或
查看答案和解析>>
科目:高中數學 來源:2012-2013學年湖北省荊州市高三10月月考理科考試數學試卷(解析版) 題型:選擇題
已知定義在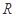 上的函數
上的函數 是奇函數且滿足
是奇函數且滿足 ,
, ,數列
,數列 滿足
滿足 ,且
,且 ,(其中
,(其中 為
為 的前
的前 項和)。則
項和)。則
A. B.
B.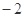 C.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2010-2011年廣東省高一期中考試數學試卷 題型:解答題
(14分)
已知定義在 上的函數
上的函數 是偶函數,且
是偶函數,且 時,
時, ,
,
(1)當 時,求
時,求 解析式;
解析式;
(2)寫出 的單調遞增區間。
的單調遞增區間。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com