中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

在△ABC中，已知c＝，b＝1，B＝30°.(1)求角A； (2)求△ABC的面積．

(1)A＝90°或A＝30°; (2)或.

解析試題分析：(1) 先由已知及正弦定理求出角Ｃ的正弦函數(shù)值，進而求得角Ｃ的大小，再由三角形的內(nèi)角和定理求出角Ａ的大小，注意角Ｃ的取值范圍及三角函數(shù)的多值性，以防漏解；(2)用兩邊及夾角正弦值積的一半求三角形的面積．
試題解析：(1)由＝得sin C＝sin B＝×sin 30°＝.
∵c>b，∴C>B，∴C＝60°或C＝120°.∴A＝90°或A＝30°.
(2)S△ABC＝bcsin A＝×1×sin 90°＝.
或S△ABC＝bcsin A＝×1××sin 30°＝.即△ABC的面積為或.
考點：1.正弦定理;2.三角形的面積.

練習(xí)冊系列答案
相關(guān)習(xí)題

科目：高中數(shù)學(xué) 來源： 題型：解答題

如圖，在△ABC中，已知∠B＝45°，D是BC邊上的一點，AD＝10，AC＝14，DC＝6，求AB的長．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

在△ABC中，a、b、c分別為角A、B、C所對的邊，且（2b+c）cosA十a(chǎn)cosC =0。
（1）求角A的大小；
（2）求的最大值，并求取得最大值時角B、C的大小．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

在△ABC中，a，b，c分別為內(nèi)角A，B，C的對邊，
且2asinA=（2b+c）sinB+（2c+b）sinC．
（1）求A的大小；
（2）求sinB+sinC的最大值．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

如圖，測量河對岸的塔高AB時，可以選與塔底B在同一水平面內(nèi)的兩個測點C與D.測得，并在點C測得塔頂A的仰角為，求塔高AB.

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

在ΔABC中，角A、B、C所對的邊分別為，且，，.
（1）求的值；（2）求ΔABC的面積.

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

設(shè)M是弧度為的∠AOB的角平分線上的一點，且OM=1，過M任作一直線與∠AOB的兩邊分別交OA、OB于點E，F(xiàn)，記∠OEM=x.
（1）若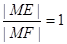時，試問x的值為多少？（2）求的取值范圍.

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

已知、、分別為的三邊、、所對的角，向量，，且.
（1）求角的大小；
（2）若，，成等差數(shù)列，且，求邊的長.

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：填空題

的三個內(nèi)角所對的邊分別為，若，
則              .

查看答案和解析>>

同步練習(xí)冊答案