已知
、
、
分別為
的三邊
、
、
所對的角，向量
，
，且
.
（1）求角的大小；
（2）若，，成等差數列，且
，求邊的長.
各地期末復習特訓卷系列答案
小博士期末闖關100分系列答案
名校名師培優作業本加核心試卷系列答案科目：高中數學 來源： 題型：解答題
如圖所示，在四邊形ABCD中，AB＝AD＝1，∠BAD＝θ，而△BCD是正三角形．
(1)將四邊形ABCD的面積S表示為θ的函數；
(2)求S的最大值及此時θ角的值．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（12分）（2011•湖北）設△ABC的內角A、B、C所對的邊分別為a、b、c，已知a=1，b=2，cosC=
（Ⅰ）求△ABC的周長；
（Ⅱ）求cos（A﹣C）的值．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
風景秀美的湖畔有四棵高大的銀杏樹，記做
、
、
、
，欲測量、兩棵樹和、兩棵樹之間的距離，但湖岸部分地方圍有鐵絲網不能靠近，現在可以方便的測得、兩點間的距離為
米，如圖，同時也能測量出
，
，
，
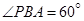，則、兩棵樹和、兩棵樹之間的距離各為多少？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
在△ABC中，內角A，B，C的對邊分別為a，b，c．已知cosA＝
，sinB＝
cosC．
(1)求tanC的值；
(2)若a＝
，求△ABC的面積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
(2) 
的值，即可確定出
，已知等式利用平面向量的數量積運算化簡，將
的值，利用余弦定理列出關系式，再利用完全平方公式變形，將
與
，
，
，所以
，而
，因此
．
，
，由（1）知
， 
，
，b＝1，B＝30°.(1)求角A； (2)求△ABC的面積．
，函數
．
的對稱中心； 
中，
分別是角
對邊，且
，且
，求
的取值范圍．
中,
.
的值;
,
,求
的長.
的三內角
、
、
所對的邊分別是
，
，
，向量
，且
。
，求
的范圍。