
 滿足條件:存在正整數
滿足條件:存在正整數 ,使得
,使得 對一切
對一切 都成立,則稱數列
都成立,則稱數列 為
為 級等比數列.
級等比數列. 為2級等比數列,且前四項分別為
為2級等比數列,且前四項分別為 ,求
,求 的值;
的值; 為常數),且
為常數),且 是
是 級等比數列,求
級等比數列,求 所有可能值的集合,并求
所有可能值的集合,并求 取最小正值時數列
取最小正值時數列 的前
的前 項和
項和 ;
; 為等比數列的充要條件是
為等比數列的充要條件是 既為
既為 級等比數列,
級等比數列, 也為
也為 級等比數列.
級等比數列.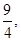 (2)
(2)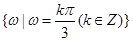 ,0,(3)詳見解析.
,0,(3)詳見解析.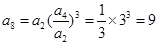 ,
,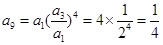 ,
,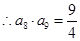 ,(2)本題化簡是關鍵.因為
,(2)本題化簡是關鍵.因為 是
是 級等比數列,所以
級等比數列,所以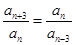
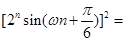
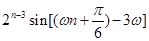
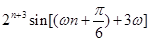
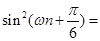
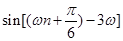

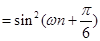
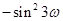
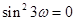 ,
,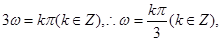
 最小正值等于
最小正值等于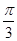 ,此時
,此時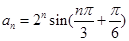
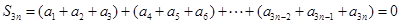 ,(3)充分性就是驗證,易證,關鍵在于證必要性,可從兩者中在交集(共同元素)出發.
,(3)充分性就是驗證,易證,關鍵在于證必要性,可從兩者中在交集(共同元素)出發. 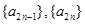 ,
, 成等比數列, 因此
成等比數列, 因此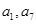 既是
既是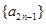 中的項,也是
中的項,也是 中的項,
中的項,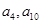 既是
既是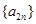 中的項,也是中
中的項,也是中 的項,可得它們公比的關系,進而推出三者結構統一,得出等比數列的結論.
的項,可得它們公比的關系,進而推出三者結構統一,得出等比數列的結論.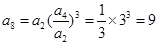 (2分)
(2分)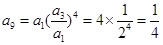
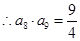 (4分)
(4分) 是
是 級等比數列,
級等比數列,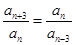
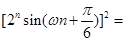
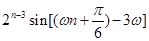
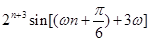 (1分)
(1分)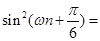
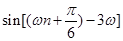

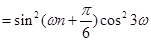

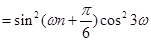

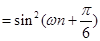
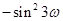
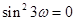 ,
,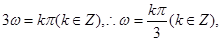
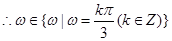 (3分)
(3分) 最小正值等于
最小正值等于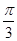 ,此時
,此時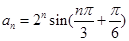
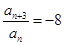 ,
,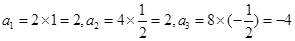 ,
,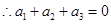
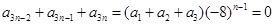 (5分)
(5分)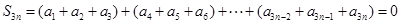 (6分)
(6分) 為等比數列,則
為等比數列,則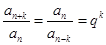
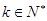 成立,顯然對
成立,顯然對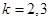 成立。
成立。 既為
既為 級等比數列,
級等比數列, 也為
也為 級等比數列。 (2分)
級等比數列。 (2分) 為
為 級等比數列,
級等比數列,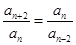 ,則
,則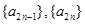 均成等比數列,設等比數列
均成等比數列,設等比數列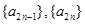 的公比分別為
的公比分別為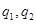 ,
, 為
為 級等比數列,
級等比數列,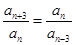 ,則
,則 成等比數列,設公比為
成等比數列,設公比為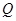 (3分)
(3分)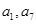 既是中
既是中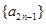 的項,也是
的項,也是 中的項,
中的項,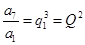
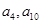 既是中
既是中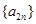 的項,也是中
的項,也是中 的項,
的項,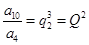
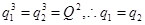 (5分)
(5分)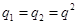 ,則
,則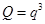
 (
(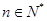 ),
),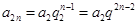 (
(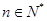 ),
),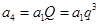 ,
,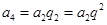 ,
, , (7分)
, (7分)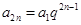 (
(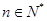 )
)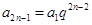 ,
,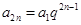 (
(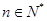 )
)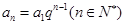 ,顯然
,顯然 為等比數列。 (8分)
為等比數列。 (8分)

 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.-1 | B.0 | C.1 | D.2 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com