

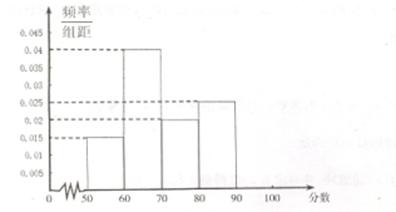
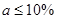
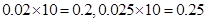 ,所以抽到的企業是優秀或良好企業的概率為0.2+0.25=0.45.
,所以抽到的企業是優秀或良好企業的概率為0.2+0.25=0.45.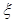 ,然后列出分布列,求出
,然后列出分布列,求出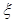 的數學期望,再由
的數學期望,再由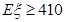 可得到關于a的不等式從而求出a的取值范圍.
可得到關于a的不等式從而求出a的取值范圍.
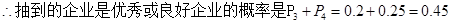
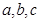 ,
,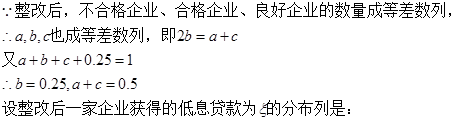

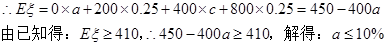 …………13分
…………13分

科目:高中數學 來源:不詳 題型:解答題

 ,
, 值,并補全頻數條形圖;
值,并補全頻數條形圖;查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 生產能力分組 |  |  |  |  |  |
| 人數 | 4 | 8 |  | 5 | 3 |
| 生產能力分組 |  |  |  |  |
| 人數 | 6 | y | 36 | 18 |
 ,再在答題紙上完成下列頻率分布直方圖。就生產能力而言,A類工人中個體間的差異程度與B類工人中個體間的差異程度哪個更小?(不用計算,可通過觀察直方圖直接回答結論)(注意:本題請在答題卡上作圖)
,再在答題紙上完成下列頻率分布直方圖。就生產能力而言,A類工人中個體間的差異程度與B類工人中個體間的差異程度哪個更小?(不用計算,可通過觀察直方圖直接回答結論)(注意:本題請在答題卡上作圖)
 類工人和
類工人和 類工人生產能力的眾數、中位數和平均數。(精確到0.1)
類工人生產能力的眾數、中位數和平均數。(精確到0.1)查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題

查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| 年人均收入(元) | 0 | 2000 | 4000 | 6000 | 8000 | 10000 | 12000 | 16000 |
| 人數(萬人) | 6 | 3 | 5 | 5 | 6 | 7 | 5 | 3 |

查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
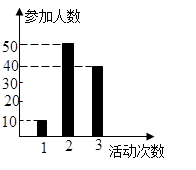
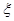 表示這兩人參加活動次數之差的絕對值,求隨機變量
表示這兩人參加活動次數之差的絕對值,求隨機變量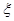 的分布列及數學期望
的分布列及數學期望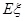 。
。查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com