中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

某公司生產產品A，產品質量按測試指標分為：指標大于或等于90為一等品，大于或等于小于為二等品，小于為三等品，生產一件一等品可盈利50元，生產一件二等品可盈利元，生產一件三等品虧損10元．現隨機抽查熟練工人甲和新工人乙生產的這種產品各100件進行檢測，檢測結果統計如下：

測試指標






甲
3
7
20
40
20
10
乙
5
15
35
35
7
3
 
現將根據上表統計得到甲、乙兩人生產產品A為一等品、二等品、三等品的頻率分別估計為他們生產產品A為一等品、二等品、三等品的概率．
（1）計算新工人乙生產三件產品A，給工廠帶來盈利大于或等于100元的概率；
（2）記甲乙分別生產一件產品A給工廠帶來的盈利和記為X，求隨機變量X的概率分布和數學期望．

（1）；（2）

解析試題分析：（1）根據上表統計得到乙兩人生產產品A為一等品、二等品、三等品的頻率分別估計為他們生產產品A為一等品、二等品、三等品的概率．由于工人乙生產三件產品A，給工廠帶來盈利大于或等于100元三種情況是：三件一等品；兩件一等品，一件二等品；一件一等品，兩件二等品；然后分別計算它們的概率并求和.
（2）由于甲乙分別生產一件產品A給工廠帶來的盈利X共有六種情況.分別求的各種情況的概率，根據數學期望公式即可得結論.
試題解析：甲生產一件產品A為一等品、二等品、三等品的概率分別為， 3分
乙生產一件產品A為一等品、二等品、三等品的概率分別為      6分
（1）新工人乙生產三件產品A，給工廠帶來盈利大于或等于100元的情形有：三件都是一等品；二件是一等品、一件是二等品或一件是一等品、二件是二等品，概率為：                8分
（2））隨機變量X的所有可能取值為100,80,60,40,20，-20．
，，
，，
，　　　
所以，隨機變量的概率分布為:


100
80
60
40
20
-20







 
隨機變量X的數學期望 （元） 12分
考點：1.統計概率.2.數學期望的計算.

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：解答題

某中學的數學測試中設置了“數學與邏輯”和“閱讀與表達”兩個內容，成績分為A、B、C、D、E五個等級。某班考生兩科的考試成績的數據統計如圖所示，其中“數學與邏輯”科目的成績等級為B的考生有10人  
（1）求該班考生中“閱讀與表達”科目中成績等級為A的人數；
（2）若等級A、B、C、D、E分別對應5分、4分、3分、2分、1分，該考場中有2人10分，3人9分，從這5人中隨機抽取2人，求2人成績之和為19分的概率.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

學校從參加高一年級期中考試的學生中抽出50名學生，并統計了他們的數學成績(成績均為整數且滿分為100分)，數學成績分組及各組頻數如下：
[40,50)，2；[50,60)，3；[60,70)，14；[70,80)，15；[80,90)，12；[90,100],4．
(1)在給出的樣本頻率分布表中，求A,B,C,D的值；
(2)估計成績在80分以上(含80分)學生的比例；
(3)為了幫助成績差的學生提高數學成績，學校決定成立“二幫一”小組，即從成績在[90,100]的學生中選兩位同學，共同幫助成績在[40,50)中的某一位同學．已知甲同學的成績為42分，乙同學的成績為95分，求甲、乙兩同學恰好被安排在同一小組的概率．樣本頻率分布表如下：

分組
頻數
頻率
[40,50)
2
0．04
[50,60)
3
0．06
[60,70)
14
0．28
[70,80)
15[]
0．30
[80,90)
A
B
[90,100]
4
0．08
合計
C
D
 

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

（本題滿分12分 ）
2013年國慶期間,高速公路車輛較多.某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(km/h)分成六段，，，，，后得到如下圖的頻率分布直方圖.
（1）此調查公司在采樣中,用到的是什么抽樣方法?
（2）求這40輛小型車輛車速的中位數的估計值；
（3）若從車速在的車輛中任抽取3輛,求抽出的3輛車中車速在的車輛數的分布列及數學期望．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

下圖為某地區2012年1月到2013年1月鮮蔬價格指數的變化情況:

記本月價格指數上月價格指數.規定：當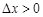時，稱本月價格指數環比增長；
當時，稱本月價格指數環比下降；當時，稱本月價格指數環比持平.
（1） 比較2012年上半年與下半年鮮蔬價格指數月平均值的大小（不要求計算過程）；
（2） 直接寫出從2012年2月到2013年1月的12個月中價格指數環比下降的月份.若從這12個月中隨機選擇連續的兩個月進行觀察，求所選兩個月的價格指數都環比下降的概率;
（3）由圖判斷從哪個月開始連續三個月的價格指數方差最大.(結論不要求證明)

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

某校高三有四個班，某次數學測試后，學校隨機地在各班抽取部分學生進行測試成績統計，各班被抽取的學生人數恰好成等差數列，人數最少的班被抽取了22人. 抽取出來的所有學生的測試成績統計結果的頻率分布條形圖如圖所示，其中120~130（包括120分但不包括130分）的頻率為0.05，此分數段的人數為5人.
（1）問各班被抽取的學生人數各為多少人？
（2）求平均成績；
（3）在抽取的所有學生中，任取一名學生，求分數不低于90分的概率.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

某城市要建成宜商、宜居的國際化現代新城，該城市的東城區、西城區分別引進8甲廠家，現對兩個區域的16個廠家進行評估，綜合得分情況如莖葉圖所示.

（1）根據莖葉圖判斷哪個區域廠家的平均分較高；
（2）規定85分以上（含85分）為優秀廠家，若從該兩個區域各選一個優秀廠家，求得分差距不超過5分的概率.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

某工廠生產、兩種元件，其質量按測試指標劃分為：大于或等于為正品，小于為次品.現從一批產品中隨機抽取這兩種元件各件進行檢測，檢測結果記錄如下：







B





由于表格被污損，數據、看不清，統計員只記得，且、兩種元件的檢測數據的平均值相等，方差也相等.
（1）求表格中與的值；
（2）從被檢測的件種元件中任取件，求件都為正品的概率.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

某食品廠對生產的某種食品按行業標準分成五個不同等級，等級系數X依次為A，B，C，D,E.現從該種食品中隨機抽取20件樣品進行檢驗，對其等級系數進行統計分析，得到頻率分布表如下：

(1)在所抽取的20件樣品中，等級系數為D的恰有3件，等級系數為E的恰有2件，求a,b,c的值；
(2)在（1)的條件下，將等級系數為D的3件樣品記為x1，x2，x3，等級系數為E的2件樣品記為y1，y2，現從x1，x2，x3，y1，y2這5件樣品中一次性任取兩件（假定每件樣品被取出的可能性相同），試寫出所有可能的結果，并求取出的兩件樣品是同一等級的概率．

查看答案和解析>>

同步練習冊答案