
如圖,儲油灌的表面積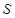 為定值,它的上部是半球,下部是圓柱,半球的半徑等于圓柱底面半徑.
為定值,它的上部是半球,下部是圓柱,半球的半徑等于圓柱底面半徑.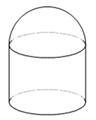
⑴試用半徑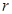 表示出儲油灌的容積
表示出儲油灌的容積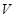 ,并寫出
,并寫出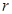 的范圍.
的范圍.
⑵當圓柱高 與半徑
與半徑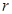 的比為多少時,儲油灌的容積
的比為多少時,儲油灌的容積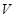 最大?
最大?
(1) (2)
(2)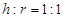
解析試題分析:(1)解決應用題問題首先要解決閱讀問題,具體說就是要會用數學式子正確表示數量關系,本題先利用儲油灌的表面積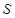 為定值得到圓柱高與半徑的關系
為定值得到圓柱高與半徑的關系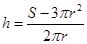 ,再根據儲油灌的容積為半球體積與圓柱體積之和,即可得儲油灌的容積
,再根據儲油灌的容積為半球體積與圓柱體積之和,即可得儲油灌的容積 的解析式;為使思路簡潔,直接用對應公式表示,根據高及半徑為正數可得
的解析式;為使思路簡潔,直接用對應公式表示,根據高及半徑為正數可得 的取值范圍,(2)本題解題思路清晰,就是利用導數求最值.難點在運算上,需用字母
的取值范圍,(2)本題解題思路清晰,就是利用導數求最值.難點在運算上,需用字母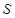 表示高
表示高 與半徑
與半徑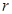 .由導數為零得
.由導數為零得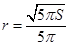 ,又由(1)得
,又由(1)得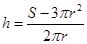 代入化簡得
代入化簡得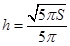 ,因此
,因此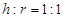 .
.
試題解析:⑴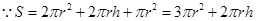 ,
,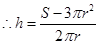 , 3分
, 3分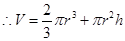
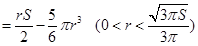 ; 7分
; 7分
⑵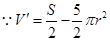 ,令
,令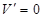 ,得
,得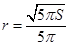 ,列表
,列表
11分
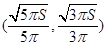
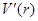
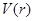
↗ 極大值即最大值 ↘
∴當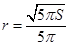 時,體積
時,體積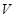 取得最大值,此時
取得最大值,此時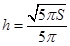 ,
,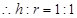 . 13分
. 13分
答:儲油灌容積 ,當
,當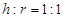 時容積
時容積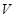 取得最大值. 15分
取得最大值. 15分
考點:圓柱側面積,球的體積,利用導數求最值


科目:高中數學 來源: 題型:解答題
如圖,四棱錐P ABCD中,PA⊥底面ABCD,PA=2
ABCD中,PA⊥底面ABCD,PA=2 ,BC="CD=2," ∠ACB=∠ACD=
,BC="CD=2," ∠ACB=∠ACD=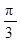 .
.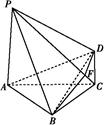
(1)求證:BD⊥平面PAC;
(2)若側棱PC上的點F滿足PF=7FC,求三棱錐P BDF的體積.
BDF的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在三棱錐S ABC中,平面EFGH分別與BC,CA,AS,SB交于點E,F,G,H,且SA⊥平面EFGH,SA⊥AB,EF⊥FG.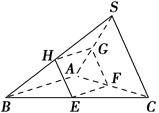
求證:(1)AB∥平面EFGH;
(2)GH∥EF;
(3)GH⊥平面SAC.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知一個四棱錐P-ABCD的三視圖(正視圖與側視圖為直角三角形,俯視圖是帶有一條對角線的正方形)如圖,E是側棱PC的中點.
(1)求四棱錐P-ABCD的體積;
(2)求證:平面APC⊥平面BDE.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在幾何體ABCDE中,∠BAC=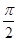 ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1。
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1。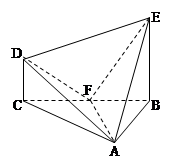
(1)設平面ABE與平面ACD的交線為直線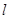 ,求證:
,求證: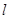 ∥平面BCDE;
∥平面BCDE;
(2)設F是BC的中點,求證:平面AFD⊥平面AFE;
(3)求幾何體ABCDE的體積。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖C,D是以AB為直徑的圓上的兩點,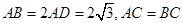 ,F是AB上的一點,且
,F是AB上的一點,且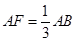 ,將圓沿AB折起,使點C在平面ABD的射影E在BD上,已知
,將圓沿AB折起,使點C在平面ABD的射影E在BD上,已知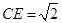
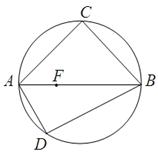
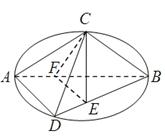
(1)求證:AD 平面BCE
平面BCE
(2)求證:AD//平面CEF;
(3)求三棱錐A-CFD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,四邊形ABCD為矩形,四邊形ADEF為梯形,AD//FE,∠AFE=60º,且平面ABCD⊥平面ADEF,AF=FE=AB= =2,點G為AC的中點.
=2,點G為AC的中點.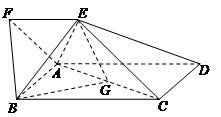
(Ⅰ)求證:EG//平面ABF;
(Ⅱ)求三棱錐B-AEG的體積;
(Ⅲ)試判斷平面BAE與平面DCE是否垂直?若垂直,請證明;若不垂直,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖, 是以
是以 為直徑的半圓上異于點
為直徑的半圓上異于點 的點,矩形
的點,矩形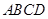 所在的平面垂直于該半圓所在平面,且
所在的平面垂直于該半圓所在平面,且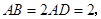
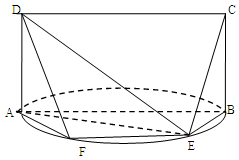
(Ⅰ)求證: ;
;
(Ⅱ)設平面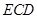 與半圓弧的另一個交點為
與半圓弧的另一個交點為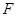 ,
,
①求證: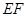 //
//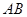 ;
;
②若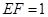 ,求三棱錐E-ADF的體積.
,求三棱錐E-ADF的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com