設函數
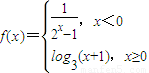
,則滿足|f(x)|<2的x的取值范圍是( )
A.(-∞,-1)∪[0,8)
B.(-∞,-1]∪[0,8]
C.(-∞,-1)(0,8)
D.(-∞,8)
【答案】
分析:由|f(x)|<2可得①
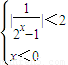
,或②
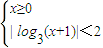
.分別求得①、②的解集,再取并集,即得所求.
解答:解:∵函數
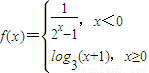
,則由|f(x)|<2可得①
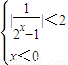
,或②
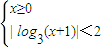
.
解①可得
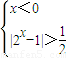
,解得 x<-1.
解②可得
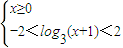
,解得 0≤x<8.
故原不等式的解集為 (-∞,-1)∪[0,8),
故選A.
點評:本題主要考查絕對值不等式的解法,體現了等價轉化和分類討論的數學而思想,屬于中檔題.
練習冊系列答案
相關習題
科目:高中數學
來源:2011-2012學年吉林省吉林市普通中學高一(上)期末數學試卷(解析版)
題型:選擇題
設函數

,則滿足f(x)=

的x值為( )
A.
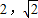
B.2
C.

D.±2
查看答案和解析>>
科目:高中數學
來源:2012-2013學年黑龍江省哈爾濱六中高三(上)期中數學試卷(理科)(解析版)
題型:選擇題
設函數
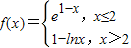
,則滿足f(x)≤1的x的取值范圍是( )
A.[1,2]
B.[0,2]
C.[1,+∞)
D.[0,+∞)
查看答案和解析>>
科目:高中數學
來源:2013-2014學年河南省鄭州47中高三(上)第一次月考數學試卷(文科)(解析版)
題型:填空題
設函數
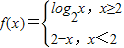
,則滿足f(x)≤2的x的取值范圍是
.
查看答案和解析>>
科目:高中數學
來源:2012-2013學年黑龍江省哈爾濱六中高三(上)期中數學試卷(理科)(解析版)
題型:選擇題
設函數
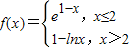
,則滿足f(x)≤1的x的取值范圍是( )
A.[1,2]
B.[0,2]
C.[1,+∞)
D.[0,+∞)
查看答案和解析>>
科目:高中數學
來源:2010年江蘇省南通市如皋市高三1月抽考數學試卷(理科)(解析版)
題型:解答題
設函數
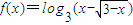
,則滿足f(x)≥0的x的取值范圍是
.
查看答案和解析>>

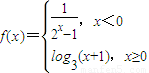 ,則滿足|f(x)|<2的x的取值范圍是( )
,則滿足|f(x)|<2的x的取值范圍是( ) 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案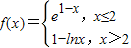 ,則滿足f(x)≤1的x的取值范圍是( )
,則滿足f(x)≤1的x的取值范圍是( )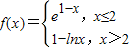 ,則滿足f(x)≤1的x的取值范圍是( )
,則滿足f(x)≤1的x的取值范圍是( )