
已知函數
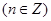 滿足
滿足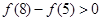 .
.
(1)求 的解析式;
的解析式;
(2)對于(1)中得到的函數 ,試判斷是否存在
,試判斷是否存在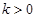 ,使
,使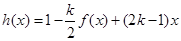 在區間
在區間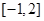 上的值域為
上的值域為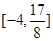 ?若存在,求出
?若存在,求出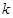 ;若不存在,請說明理由.
;若不存在,請說明理由.
科目:高中數學 來源: 題型:解答題
對于定義域為A的函數f(x),如果任意的x1,x2∈A,當x1<x2時,都有f(x1)<f(x2),則稱函數f(x)是A上的嚴格增函數;函數f(k)是定義在N*上,函數值也在N*中的嚴格增函數,并且滿足條件f(f(k))=3k.
(1)證明:f(3k)=3f(k);
(2)求f(3k-1)(k∈N*)的值;
(3)是否存在p個連續的自然數,使得它們的函數值依次也是連續的自然數;若存在,找出所有的p值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知 是正數,
是正數, ,
, ,
, .
.
(Ⅰ)若 成等差數列,比較
成等差數列,比較 與
與 的大小;
的大小;
(Ⅱ)若 ,則
,則 三個數中,哪個數最大,請說明理由;
三個數中,哪個數最大,請說明理由;
(Ⅲ)若 ,
, ,
, (
( ),且
),且 ,
, ,
, 的整數部分分別是
的整數部分分別是

 求所有
求所有 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
己知函數f(x)=ex,x R.
R.
(1)若直線y=kx+1與f(x)的反函數圖象相切,求實數k的值;
(2)設x﹥0,討論曲線y=f(x)與曲線y=mx2(m﹥0)公共點的個數;
(3)設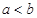 ,比較
,比較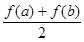 與
與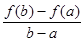 的大小并說明理由。
的大小并說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某產品生產廠家根據以往的生產銷售經驗得到下面有關生產銷售的統計規律:每生產產品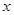 (百臺),其總成本為
(百臺),其總成本為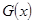 (萬元),其中固定成本為2.8萬元,并且每生產1百臺的生產成本為1萬元(總成本=固定成本+生產成本)。銷售收入
(萬元),其中固定成本為2.8萬元,并且每生產1百臺的生產成本為1萬元(總成本=固定成本+生產成本)。銷售收入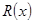 (萬元)滿足
(萬元)滿足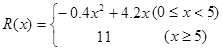 ,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題:
,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題:
分別寫出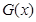 和利潤函數
和利潤函數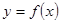 的解析式(利潤=銷售收入—總成本);
的解析式(利潤=銷售收入—總成本);
工廠生產多少臺產品時,可使盈利最多?并求出此時每臺產品的售價。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com