
某產(chǎn)品生產(chǎn)廠家根據(jù)以往的生產(chǎn)銷(xiāo)售經(jīng)驗(yàn)得到下面有關(guān)生產(chǎn)銷(xiāo)售的統(tǒng)計(jì)規(guī)律:每生產(chǎn)產(chǎn)品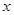 (百臺(tái)),其總成本為
(百臺(tái)),其總成本為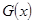 (萬(wàn)元),其中固定成本為2.8萬(wàn)元,并且每生產(chǎn)1百臺(tái)的生產(chǎn)成本為1萬(wàn)元(總成本=固定成本+生產(chǎn)成本)。銷(xiāo)售收入
(萬(wàn)元),其中固定成本為2.8萬(wàn)元,并且每生產(chǎn)1百臺(tái)的生產(chǎn)成本為1萬(wàn)元(總成本=固定成本+生產(chǎn)成本)。銷(xiāo)售收入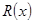 (萬(wàn)元)滿足
(萬(wàn)元)滿足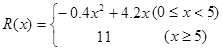 ,假定該產(chǎn)品產(chǎn)銷(xiāo)平衡(即生產(chǎn)的產(chǎn)品都能賣(mài)掉),根據(jù)上述統(tǒng)計(jì)規(guī)律,請(qǐng)完成下列問(wèn)題:
,假定該產(chǎn)品產(chǎn)銷(xiāo)平衡(即生產(chǎn)的產(chǎn)品都能賣(mài)掉),根據(jù)上述統(tǒng)計(jì)規(guī)律,請(qǐng)完成下列問(wèn)題:
分別寫(xiě)出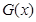 和利潤(rùn)函數(shù)
和利潤(rùn)函數(shù)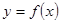 的解析式(利潤(rùn)=銷(xiāo)售收入—總成本);
的解析式(利潤(rùn)=銷(xiāo)售收入—總成本);
工廠生產(chǎn)多少臺(tái)產(chǎn)品時(shí),可使盈利最多?并求出此時(shí)每臺(tái)產(chǎn)品的售價(jià)。
(1)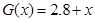 ,
, =R(x)-G(x)=
=R(x)-G(x)=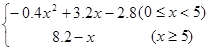 ;(2)當(dāng)工廠生產(chǎn)4百臺(tái)時(shí),可使贏利最多,此時(shí)每臺(tái)售價(jià)為260元.
;(2)當(dāng)工廠生產(chǎn)4百臺(tái)時(shí),可使贏利最多,此時(shí)每臺(tái)售價(jià)為260元.
解析試題分析:(1)由題意總成本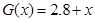 ,利潤(rùn)函數(shù)
,利潤(rùn)函數(shù)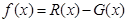 ;(2)要使盈利最多,即求函數(shù)
;(2)要使盈利最多,即求函數(shù) 的最大值,分段函數(shù)在每一段上分別求最大值,當(dāng)
的最大值,分段函數(shù)在每一段上分別求最大值,當(dāng)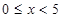 時(shí),由二次函數(shù)性質(zhì)求得
時(shí),由二次函數(shù)性質(zhì)求得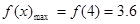 ,當(dāng)
,當(dāng)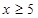 時(shí),
時(shí),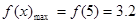 ,因此當(dāng)
,因此當(dāng)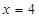 時(shí),
時(shí), 取得最大值3.6 , 此時(shí)每臺(tái)售價(jià)為
取得最大值3.6 , 此時(shí)每臺(tái)售價(jià)為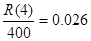 (萬(wàn)元)=260元.
(萬(wàn)元)=260元.
試題解析:(1)由題意得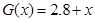 . 2分
. 2分
∴ =
=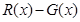 =
=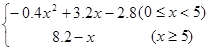
 .5分
.5分
(2)當(dāng)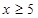 時(shí),函數(shù)
時(shí),函數(shù) 在
在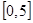 上單調(diào)遞減,
上單調(diào)遞減, 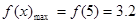 7分
7分
當(dāng)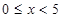 時(shí),函數(shù)
時(shí),函數(shù) =-0.4(x-4)2+3.6,
=-0.4(x-4)2+3.6,
當(dāng)x=4時(shí),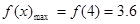 10分
10分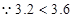
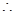 當(dāng)
當(dāng)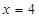 時(shí),
時(shí), 取得最大值3.6 11分
取得最大值3.6 11分
此時(shí)每臺(tái)售價(jià)為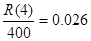 (萬(wàn)元)=260元 13分
(萬(wàn)元)=260元 13分
答:當(dāng)工廠生產(chǎn)4百臺(tái)時(shí),可使贏利最多,此時(shí)每臺(tái)售價(jià)為260元 . 15分
考點(diǎn):1、分段函數(shù)的解析式;2、分段函數(shù)的最值的求法.


 習(xí)題精選系列答案
習(xí)題精選系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)
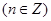 滿足
滿足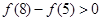 .
.
(1)求 的解析式;
的解析式;
(2)對(duì)于(1)中得到的函數(shù) ,試判斷是否存在
,試判斷是否存在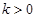 ,使
,使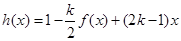 在區(qū)間
在區(qū)間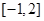 上的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/a3/9/18b9s3.png" style="vertical-align:middle;" />?若存在,求出
上的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/a3/9/18b9s3.png" style="vertical-align:middle;" />?若存在,求出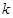 ;若不存在,請(qǐng)說(shuō)明理由.
;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
某企業(yè)生產(chǎn)某種商品 噸,此時(shí)所需生產(chǎn)費(fèi)用為(
噸,此時(shí)所需生產(chǎn)費(fèi)用為(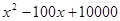 )萬(wàn)元,當(dāng)出售這種商品時(shí),每噸價(jià)格為
)萬(wàn)元,當(dāng)出售這種商品時(shí),每噸價(jià)格為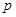 萬(wàn)元,這里
萬(wàn)元,這里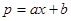 (
(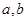 為常數(shù),
為常數(shù),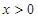 )
)
(1)為了使這種商品的生產(chǎn)費(fèi)用平均每噸最低,那么這種商品的產(chǎn)量應(yīng)為多少?lài)崳?br />(2)如果生產(chǎn)出來(lái)的商品能全部賣(mài)完,當(dāng)產(chǎn)量是120噸時(shí)企業(yè)利潤(rùn)最大,此時(shí)出售價(jià)格是每噸160萬(wàn)元,求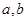 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)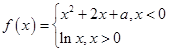 ,其中
,其中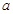 是實(shí)數(shù),設(shè)
是實(shí)數(shù),設(shè)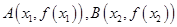 為該函數(shù)的圖象上的兩點(diǎn),且
為該函數(shù)的圖象上的兩點(diǎn),且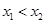 .
.
⑴指出函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
⑵若函數(shù) 的圖象在點(diǎn)
的圖象在點(diǎn)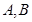 處的切線互相垂直,且
處的切線互相垂直,且 ,求
,求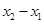 的最小值;
的最小值;
⑶若函數(shù) 的圖象在點(diǎn)
的圖象在點(diǎn)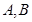 處的切線重合,求
處的切線重合,求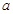 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
運(yùn)貨卡車(chē)以每小時(shí) 千米的速度勻速行駛130千米
千米的速度勻速行駛130千米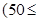
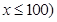 (單位:千米/小時(shí)).假設(shè)汽油的價(jià)格是每升2元,而汽車(chē)每小時(shí)耗油
(單位:千米/小時(shí)).假設(shè)汽油的價(jià)格是每升2元,而汽車(chē)每小時(shí)耗油 升,司機(jī)的工資是每小時(shí)14元.
升,司機(jī)的工資是每小時(shí)14元.
(1)求這次行車(chē)總費(fèi)用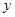 關(guān)于
關(guān)于 的表達(dá)式;
的表達(dá)式;
(2)當(dāng) 為何值時(shí),這次行車(chē)的總費(fèi)用最低,并求出最低費(fèi)用的值.
為何值時(shí),這次行車(chē)的總費(fèi)用最低,并求出最低費(fèi)用的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知二次函數(shù)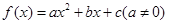 的圖像頂點(diǎn)為
的圖像頂點(diǎn)為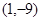 ,且圖像在
,且圖像在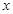 軸截得的線段長(zhǎng)為6.
軸截得的線段長(zhǎng)為6.
(Ⅰ)求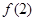 ;
;
(Ⅱ)若 在區(qū)間
在區(qū)間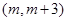 上單調(diào),求
上單調(diào),求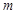 的范圍.
的范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知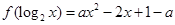 ,
,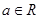 .
.
(1)求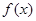 的解析式;
的解析式;
(2)解關(guān)于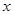 的方程
的方程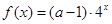
(3)設(shè)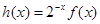 ,
,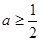 時(shí),對(duì)任意
時(shí),對(duì)任意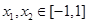 總有
總有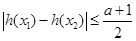 成立,求
成立,求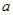 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
某種汽車(chē)的購(gòu)車(chē)費(fèi)用是10萬(wàn)元,每年使用的保險(xiǎn)費(fèi)、養(yǎng)路費(fèi)、汽油費(fèi)約為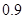 萬(wàn)元,年維修費(fèi)用第一年是
萬(wàn)元,年維修費(fèi)用第一年是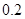 萬(wàn)元,第二年是
萬(wàn)元,第二年是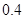 萬(wàn)元,第三年是
萬(wàn)元,第三年是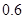 萬(wàn)元,…,以后逐年遞增
萬(wàn)元,…,以后逐年遞增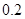 萬(wàn)元汽車(chē)的購(gòu)車(chē)費(fèi)用、每年使用的保險(xiǎn)費(fèi)、養(yǎng)路費(fèi)、汽油費(fèi)、維修費(fèi)用的和平均攤到每一年的費(fèi)用叫做年平均費(fèi)用.設(shè)這種汽車(chē)使用
萬(wàn)元汽車(chē)的購(gòu)車(chē)費(fèi)用、每年使用的保險(xiǎn)費(fèi)、養(yǎng)路費(fèi)、汽油費(fèi)、維修費(fèi)用的和平均攤到每一年的費(fèi)用叫做年平均費(fèi)用.設(shè)這種汽車(chē)使用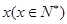 年的維修費(fèi)用的和為
年的維修費(fèi)用的和為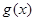 ,年平均費(fèi)用為
,年平均費(fèi)用為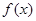 .
.
(1)求出函數(shù)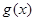 ,
,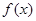 的解析式;
的解析式;
(2)這種汽車(chē)使用多少年時(shí),它的年平均費(fèi)用最小?最小值是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知二次函數(shù)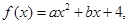 集合
集合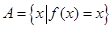
(1)若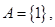 求函數(shù)
求函數(shù) 的解析式;
的解析式;
(2)若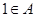 ,且
,且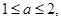 設(shè)
設(shè) 在區(qū)間
在區(qū)間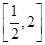 上的最大值、最小值分別為
上的最大值、最小值分別為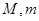 ,記
,記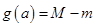 ,求
,求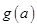 的最小值.
的最小值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com