
在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,點D在棱AB上.
(1)若D是AB中點,求證:AC1∥平面B1CD;
(2)當(dāng) 時,求二面角
時,求二面角 的余弦值.
的余弦值.
(1)詳見解析;(2)
解析試題分析:(1)要證明AC1∥平面B1CD,根據(jù)線面的判定定理,只要轉(zhuǎn)換證明DE//AC1即可;
(2)可以以C為原點建立空間直角坐標(biāo)系,求出平面BCD的法向量與平面B1CD的法向量,然后利用向量夾角公式即可.
試題解析:解:(1)證明:連結(jié)BC1,交B1C于E,連接DE.
因為直三棱柱ABC-A1B1C1,D是AB中點,
所以側(cè)面BB1C1C為矩形,DE為△ABC1的中位線,所以DE//AC1.
因為DE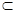 平面B1CD,AC1
平面B1CD,AC1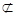 平面B1CD,所以AC1∥平面B1CD.6分
平面B1CD,所以AC1∥平面B1CD.6分
(2)由(1)知AC⊥BC,如圖,以C為原點建立空間直角坐標(biāo)系C-xyz.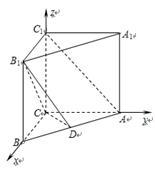
則B(3,0,0),A(0,4,0),A1(0,4,4),B1(3,0,4).設(shè)D(a,b,0)(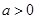 ,
,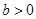 ),因為點D在線段AB上,且
),因為點D在線段AB上,且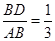 ,即
,即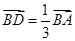 .
.
所以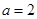 ,
,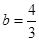 ,
,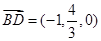 ,
,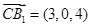 ,
,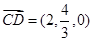 .
.
平面BCD的法向量為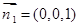 .設(shè)平面B1CD的法向量為
.設(shè)平面B1CD的法向量為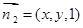 ,
,
由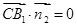 ,
, ,得
,得 ,
,
所以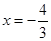 ,
,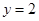 ,
,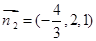 .所以
.所以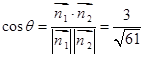 .
.
所以二面角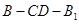 的余弦值為
的余弦值為 .12分
.12分
考點:(1)空間位置關(guān)系的證明;(2)平面向量在立體幾何中的應(yīng)用.


科目:高中數(shù)學(xué) 來源: 題型:解答題
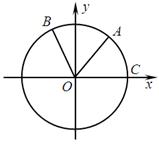
如圖,點A、B是單位圓 上的兩點,點C是圓
上的兩點,點C是圓 與
與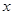 軸的正半軸的交點,將銳角
軸的正半軸的交點,將銳角 的終邊
的終邊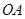 按逆時針方向旋轉(zhuǎn)
按逆時針方向旋轉(zhuǎn) 到
到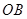 .
.
(1)若點A的坐標(biāo)為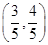 ,求
,求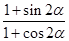 的值;
的值;
(2)用 表示
表示 ,并求
,并求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,A,B是海面上位于東西方向相距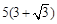 海里的兩個觀測點,現(xiàn)位于A點北偏東45°,B點北偏西60°的D點有一艘輪船發(fā)出求救信號,位于B點南偏西60°且與B點相距
海里的兩個觀測點,現(xiàn)位于A點北偏東45°,B點北偏西60°的D點有一艘輪船發(fā)出求救信號,位于B點南偏西60°且與B點相距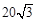 海里的C點的救援船立即即前往營救,其航行速度為30海里/小時,該救援船到達(dá)D點需要多長時間?
海里的C點的救援船立即即前往營救,其航行速度為30海里/小時,該救援船到達(dá)D點需要多長時間?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖所示,某旅游景點有一座風(fēng)景秀麗的山峰,山上有一條筆直的山路BC和一條索道AC,小王和小李打算不坐索道,而是花2個小時的時間進(jìn)行徒步攀登.已知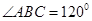 ,
,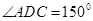 ,
,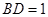 (千米),
(千米),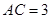 (千米).假設(shè)小王和小李徒步攀登的速度為每小時1200米,請問:兩位登山愛好者能否在2個小時內(nèi)徒步登上山峰.
(千米).假設(shè)小王和小李徒步攀登的速度為每小時1200米,請問:兩位登山愛好者能否在2個小時內(nèi)徒步登上山峰.
(即從B點出發(fā)到達(dá)C點)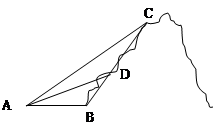
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在△ABC中,a,b,c分別為角A,B,C的對邊,
(1)求角A的度數(shù);
(2)若a= ,b+c=3,求△ABC的面積.
,b+c=3,求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在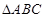 中,角A、B、C的對邊分別為a、b、c,且角A、B、C成等差教列.(1)若
中,角A、B、C的對邊分別為a、b、c,且角A、B、C成等差教列.(1)若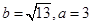 ,求邊c的值;
,求邊c的值;
(2)設(shè)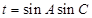 ,求t的最大值.
,求t的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知向量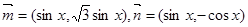 ,設(shè)函數(shù)
,設(shè)函數(shù)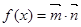 ,若函數(shù)
,若函數(shù)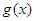 的圖象與
的圖象與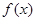 的圖象關(guān)于坐標(biāo)原點對稱.
的圖象關(guān)于坐標(biāo)原點對稱.
(1)求函數(shù)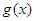 在區(qū)間
在區(qū)間 上的最大值,并求出此時
上的最大值,并求出此時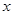 的取值;
的取值;
(2)在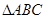 中,
中,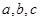 分別是角
分別是角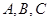 的對邊,若
的對邊,若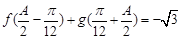 ,
,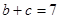 ,
,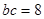 ,求邊
,求邊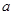 的長.
的長.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com