
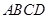 的外接球的球心為
的外接球的球心為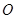 ,
,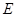 是
是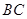 的中點,則直線
的中點,則直線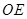 和平面
和平面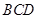 所成角的正切值為 。
所成角的正切值為 。 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:不詳 題型:解答題
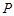 為斜三棱柱
為斜三棱柱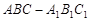 的側棱
的側棱 上一點,
上一點,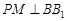 交
交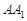 于點
于點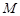 ,
,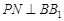 交
交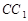 于點
于點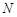 .
.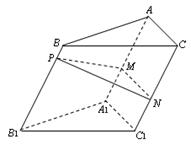
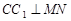 ;
;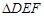 中有余弦定理:
中有余弦定理: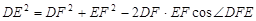 . 拓展到空間,類比三角形的余弦定理,寫出斜三棱柱的三個側面面積與其中兩個側面所成的二面角之間的關系式(只寫結論,不必證明)
. 拓展到空間,類比三角形的余弦定理,寫出斜三棱柱的三個側面面積與其中兩個側面所成的二面角之間的關系式(只寫結論,不必證明)查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
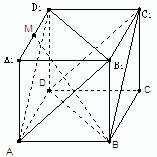
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.直線a平行于平面M,則a平行于M內的任意一條直線 |
| B.直線a與平面M相交,則a不平行于M內的任意一條直線 |
| C.直線a不垂直于平面M,則a不垂直于M內的任意一條直線 |
| D.直線a不垂直于平面M,則過a的平面不垂直于M |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
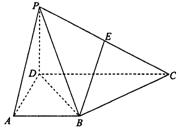
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com