
已知數列{an}滿足a1=3,an+1=an+p·3n(n∈N*,p為常數),a1,a2+6,a3成等差數列.
(1)求p的值及數列{an}的通項公式;
(2)設數列{bn}滿足bn=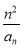 ,證明:bn≤
,證明:bn≤ .
.
(1)an=3n(2)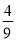
【解析】由a1=3,an+1=an+p·3n,得a2=3+3p,a3=a2+9p=3+12p.
∵a1,a2+6,a3成等差數列,∴a1+a3=2(a2+6),即3+3+12p=2(3+3p+6),得p=2.
依題意知,an+1=an+2×3n,
當n≥2時,a2-a1=2×31,a3-a2=2×32,…,an-an-1=2×3n-1.
等號兩邊分別相加得an-a1=2(31+32+…+3n-1)=2×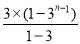 =3n-3,
=3n-3,
∴an-a1=3n-3,∴an=3n(n≥2).
又a1=3適合上式,故an=3n.
(2)證明:∵an=3n,∴bn=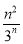 .
.
∵bn+1-bn=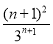 -
-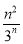 =
=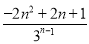 (n∈N*).
(n∈N*).
若-2n2+2n+1<0,則n> ,
,
即當n≥2時,有bn+1<bn.
又因為b1=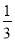 ,b2<
,b2<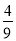 .故bn≤
.故bn≤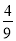


科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練倒數第10天練習卷(解析版) 題型:選擇題
已知集合M={a,b,c},集合N滿足N⊆M,則集合N的個數是( ).
A.6 B.7 C.8 D.9
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練3-x4練習卷(解析版) 題型:選擇題
已知某8個數的平均數為5,方差為2,現又加入一個新數據5,此時這9個數的平均數為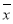 ,方差為s2,則( ).
,方差為s2,則( ).
A.  =5,s2<2 B.
=5,s2<2 B.  =5,s2>2 C.
=5,s2>2 C.  >5,s2<2 D.
>5,s2<2 D.  >5,s2>2
>5,s2>2
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練3-x1練習卷(解析版) 題型:選擇題
正四棱錐S-ABCD的側棱長為 ,底面邊長為
,底面邊長為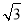 ,E為SA的中點,則異面直線BE和SC所成的角為( ).
,E為SA的中點,則異面直線BE和SC所成的角為( ).

A.30° B.45° C.60° D.90°
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練3-d4練習卷(解析版) 題型:解答題
設數列{an}的前n項和為Sn,a1=1,且對任意正整數n,點(an+1,Sn)在直線3x+2y-3=0上.
(1)求數列{an}的通項公式;
(2)是否存在實數λ,使得數列 為等差數列?若存在,求出λ的值;若不存在,則說明理由.
為等差數列?若存在,求出λ的值;若不存在,則說明理由.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練2-2練習卷(解析版) 題型:解答題
某次考試中,從甲,乙兩個班各抽取10名學生的成績進行統計分析,兩班10名學生成績的莖葉圖如圖所示,成績不小于90分為及格.

(1)從每班抽取的學生中各抽取一人,求至少有一個及格的概率;
(2)從甲班10人中取兩人,乙班10人中取一人,三人中及格人數記為X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練2-1練習卷(解析版) 題型:解答題
在△ABC中,角A,B,C的對邊分別為a,b,c,已知角A= , sin B=3sin C.
, sin B=3sin C.
(1)求tan C的值;
(2)若a= ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練1-9練習卷(解析版) 題型:填空題
如圖,橢圓 =1(a>b>0)的左、右焦點為F1,F2,上頂點為A,離心率為
=1(a>b>0)的左、右焦點為F1,F2,上頂點為A,離心率為 ,點P為第一象限內橢圓上的一點,若S△PF1A∶S△PF1F2=2∶1,則直線PF1的斜率為________.
,點P為第一象限內橢圓上的一點,若S△PF1A∶S△PF1F2=2∶1,則直線PF1的斜率為________.

查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習體系通關訓練1-7練習卷(解析版) 題型:選擇題
已知集合A= ,B={x||x-1|≤1},則A∩B=( ).
,B={x||x-1|≤1},則A∩B=( ).
A.{-1,0} B.{0,1} C.{0} D.{1}
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com