
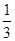 x3+ax2+bx(a,b∈R).
x3+ax2+bx(a,b∈R).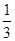 ,且函數f(x)在
,且函數f(x)在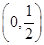 上不存在極值點,求a的取值范圍.
上不存在極值點,求a的取值范圍.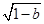 ),(-1+
),(-1+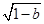 ,+∞);減區間為(-1-
,+∞);減區間為(-1-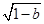 ,-1+
,-1+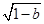 ).(2)(-∞,0]
).(2)(-∞,0]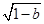 )(x+1-
)(x+1-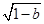 ),
),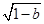 ),(-1+
),(-1+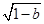 ,+∞)上為增函數,f(x)在(-1-
,+∞)上為增函數,f(x)在(-1-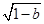 ,-1+
,-1+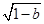 )上為減函數.
)上為減函數.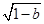 ),(-1+
),(-1+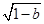 ,+∞),減區間為(-1-
,+∞),減區間為(-1-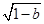 ,-1+
,-1+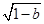 ).
).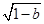 ),(-1+
),(-1+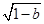 ,+∞);減區間為(-1-
,+∞);減區間為(-1-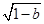 ,-1+
,-1+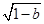 ).
).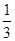 ,得b=-a,
,得b=-a,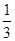 x3+ax2-ax,f′(x)=x2+2ax-a.
x3+ax2-ax,f′(x)=x2+2ax-a.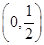 ,所以a=
,所以a=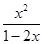 .
.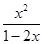 =
=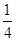
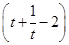 .
. -2在t∈(0,1)上單調遞減,故h(t)∈(0,+∞).
-2在t∈(0,1)上單調遞減,故h(t)∈(0,+∞).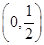 上不存在極值點,得a=
上不存在極值點,得a=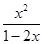 在
在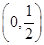 上無解,所以,a∈(-∞,0].
上無解,所以,a∈(-∞,0].

科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
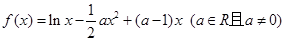
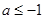 時,求函數
時,求函數 的單調遞增區間;
的單調遞增區間;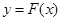 的圖象為曲線
的圖象為曲線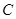 ,設點
,設點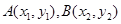 是曲線
是曲線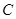 上的不同兩點.如果在曲線
上的不同兩點.如果在曲線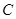 上存在點
上存在點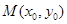 ,使得:①
,使得:①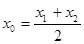 ;②曲線
;②曲線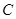 在點
在點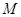 處的切線平行于直線
處的切線平行于直線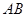 ,則稱函數
,則稱函數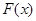 存在“中值相依切線”,試問:函數
存在“中值相依切線”,試問:函數 是否存在“中值相依切線”,請說明理由.
是否存在“中值相依切線”,請說明理由.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
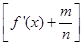 (f′(x)是f(x)的導函數)在區間(t,3)上總不是單調函數,求m的取值范圍;
(f′(x)是f(x)的導函數)在區間(t,3)上總不是單調函數,求m的取值范圍;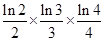 ×…×
×…×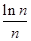 <
<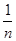 (n≥2,n∈N*)
(n≥2,n∈N*)查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
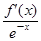 -a-2,h(x)=
-a-2,h(x)=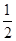 x2-2x-ln x,若x>1時總有g(x)<h(x),求實數a的取值范圍.
x2-2x-ln x,若x>1時總有g(x)<h(x),求實數a的取值范圍.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
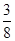 時,判斷方程f(x)=-
時,判斷方程f(x)=-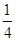 的實數根的個數,并說明理由.
的實數根的個數,并說明理由.查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
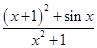 ,其導函數記為f′(x),則f(2 012)+f′(2 012)+f(-2012)-f′(-2012)=________.
,其導函數記為f′(x),則f(2 012)+f′(2 012)+f(-2012)-f′(-2012)=________.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com