
實數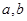 是分別從集合A={1,2,3,4}中隨機抽取的元素,集合B=
是分別從集合A={1,2,3,4}中隨機抽取的元素,集合B=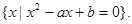
(1)寫出使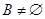 的所有實數對
的所有實數對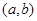
(2)求隨機抽取的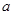 與
與 的值滿足
的值滿足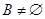 且
且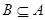 的概率.
的概率.
(1)(2,1)(3,1)(3,2)(4,1)(4,2)(4,3)(4,4);(2)P=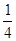 。
。
解析試題分析:(1)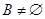 也就是
也就是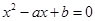 有根,因而可知
有根,因而可知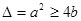 ,再結合a,b從集合A中取值可得滿足條件的實數對
,再結合a,b從集合A中取值可得滿足條件的實數對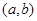 .
.
(2)根據(1)可知(a,b)共有16組,然后找出滿足條件的有4組,根據古典概型概率計算公式計算即可.
(1)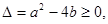 即
即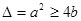 ,則B
,則B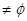 時
時
(a,b)是:(2,1)(3,1)(3,2)(4,1)(4,2)(4,3)(4,4)……6分
(2)(a,b)共有16組,其中滿足條件有:(2,1)(3,2)(4,3)(4,4)4組,P=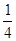 ……12分
……12分
考點:集合的定義及表示,集合間的包含關系,古典概型的概率問題.
點評:掌握集合的概念及其表示方法,以及集合之間的包含關系是解決本題的突破口,然后再計算概率時要注意本小題屬于古典概型概率問題.


 小學奪冠AB卷系列答案
小學奪冠AB卷系列答案 ABC考王全優卷系列答案
ABC考王全優卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com