Question

（本小題滿分12分）
定義在R上的偶函數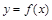在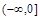上遞增，函數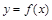的一個零點為－。
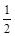求滿足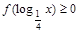的x的取值集合．

Answer 1

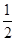{x|≤x≤2}

解析試題分析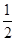：　∵－是函數的零點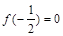，∴，…………………………………1分
∵為偶函數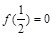，∴，…………………………………2分
∵在(－∞，0]上遞增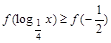，…………………………4分
∴0≥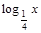≥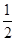－，∴1≤x≤2，…………………………………7分
∵為偶函數，∴在[0，＋∞)上單調減，…………………………………8分
又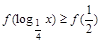，∴0≤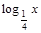≤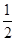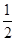，∴≤x≤1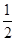，∴≤x≤2.………………11分
故x的取值集合為{x|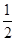≤x≤2}．…………………………………12分
考點：本試題考查了函數的零點以及對數不等式的求解運用。
點評：解決該試題的關鍵是利用函數的零點，轉化為該數是方程的一個根，進而根據偶函數求解得到函數值為零的點，然后結合單調性來得到不等式的解集。屬于中檔題。 易錯點是對數不等式的求解，忽略了單調性造成不等式符號的錯誤 。