
“城中觀海”是近年來國內很多大中型城市內澇所致的現象,究其原因,除天氣因素、城市規劃等原因外,城市垃圾雜物也是造成內澇的一個重要原因。暴雨會沖刷城市的垃圾雜物一起進入下水道,據統計,在不考慮其它因素的條件下,某段下水道的排水量V(單位:立方米/小時)是雜物垃圾密度x(單位:千克/立方米)的函數。當下水道的垃圾雜物密度達到2千克/立方米時,會造成堵塞,此時排水量為0;當垃圾雜物密度不超過0.2千克/立方米時,排水量是90立方米/小時;研究表明,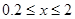 時,排水量V是垃圾雜物密度x的一次函數。
時,排水量V是垃圾雜物密度x的一次函數。
(Ⅰ)當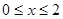 時,求函數V(x)的表達式;
時,求函數V(x)的表達式;
(Ⅱ)當垃圾雜物密度x為多大時,垃圾雜物量(單位時間內通過某段下水道的垃圾雜物量,單位:千克/小時) 可以達到最大,求出這個最大值。
可以達到最大,求出這個最大值。
(Ⅰ) ;(Ⅱ)當雜物垃圾密度
;(Ⅱ)當雜物垃圾密度 千克/立方米,f(x)取得最大值50千克/小時.
千克/立方米,f(x)取得最大值50千克/小時.
解析試題分析:(Ⅰ)當下水道的垃圾雜物密度達到2千克/立方米時,會造成堵塞,此時排水量為0;當垃圾雜物密度不超過0.2千克/立方米時,排水量是90立方米/小時說明函數圖像過 ,與
,與 ,又因為當
,又因為當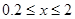 時,排水量V是垃圾雜物密度x的一次函數,可設
時,排水量V是垃圾雜物密度x的一次函數,可設 ,將
,將 與
與 代入可求出
代入可求出 ,而在
,而在 ,
, ,從而得
,從而得 的解析式;(Ⅱ)當垃圾雜物密度x為多大時,垃圾雜物量
的解析式;(Ⅱ)當垃圾雜物密度x為多大時,垃圾雜物量 可以達到最大,由
可以達到最大,由 ,這是一個分段函數,分段函數的最值分段求,然后比較誰最大為誰,當
,這是一個分段函數,分段函數的最值分段求,然后比較誰最大為誰,當 ,是一個一次函數,當
,是一個一次函數,當 時最大,最大值為
時最大,最大值為 ,當
,當 ,這是一個二次函數,對稱軸為
,這是一個二次函數,對稱軸為 ,故
,故 時最大,最大值為
時最大,最大值為 ,從而得當雜物垃圾密度
,從而得當雜物垃圾密度 千克/立方米,f(x)取得最大值50千克/小時.
千克/立方米,f(x)取得最大值50千克/小時.
試題解析:(Ⅰ)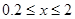 時,排水量V是垃圾雜物密度x的一次函數,設為
時,排水量V是垃圾雜物密度x的一次函數,設為 ,將
,將 與
與 代入得
代入得 ,
, (6分)
(6分)
(Ⅱ)
 千克/小時
千克/小時 ,
,
所以,當雜物垃圾密度 千克/立方米,f(x)取得最大值50千克/小時。(13分)
千克/立方米,f(x)取得最大值50千克/小時。(13分)
分)
考點:應用題,分段函數最值.


 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:解答題
集合A是由適合以下性質的函數 構成的:對于定義域內任意兩個不相等的實數
構成的:對于定義域內任意兩個不相等的實數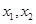 ,都有
,都有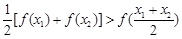 .
.
(1)試判斷 =
=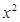 及
及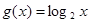 是否在集合A中,并說明理由;
是否在集合A中,并說明理由;
(2)設 ÎA且定義域為(0,+¥),值域為(0,1),
ÎA且定義域為(0,+¥),值域為(0,1), ,試寫出一個滿足以上條件的函數
,試寫出一個滿足以上條件的函數 的解析式,并給予證明.
的解析式,并給予證明.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某分公司經銷某種品牌產品,每件產品的成本為30元,并且每件產品須向總公司繳納a元(a為常數,2≤a≤5)的管理費,根據多年的統計經驗,預計當每件產品的售價為x元時,產品一年的銷售量為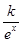 (e為自然對數的底數)萬件,已知每件產品的售價為40元時,該產品一年的銷售量為500萬件.經物價部門核定每件產品的售價x最低不低于35元,最高不超過41元.
(e為自然對數的底數)萬件,已知每件產品的售價為40元時,該產品一年的銷售量為500萬件.經物價部門核定每件產品的售價x最低不低于35元,最高不超過41元.
(Ⅰ)求分公司經營該產品一年的利潤L(x)萬元與每件產品的售價x元的函數關系式;
(Ⅱ)當每件產品的售價為多少元時,該產品一年的利潤L(x)最大,并求出L(x)的最大值.
參考公式: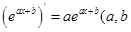 為常數
為常數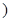 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知某公司生產品牌服裝的年固定成本為10萬元,每生產千件,須另投入2.7萬元,設該公司年內共生產品牌服裝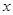 千件并全部銷售完,每千件的銷售收入為
千件并全部銷售完,每千件的銷售收入為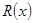 萬元,且
萬元,且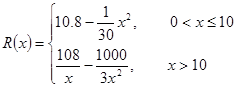 .
.
(1)寫出年利潤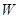 (萬元)關于年產量
(萬元)關于年產量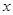 (千件)的函數解析式;
(千件)的函數解析式;
(2)當年產量為多少千件時,該公司在這一品牌服裝的生產中所獲年利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某跳水運動員在一次跳水訓練時的跳水曲線為如圖所示的拋物線一段,已知跳水板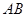 長為2m,跳水板距水面
長為2m,跳水板距水面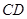 的高
的高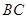 為3m,
為3m, =5m,
=5m,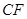 =6m,為安全和空中姿態優美,訓練時跳水曲線應在離起跳點
=6m,為安全和空中姿態優美,訓練時跳水曲線應在離起跳點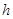 m(
m(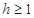 )時達到距水面最大高度4m,規定:以
)時達到距水面最大高度4m,規定:以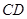 為橫軸,
為橫軸, 為縱軸建立直角坐標系.
為縱軸建立直角坐標系.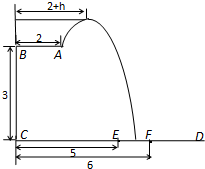
(1)當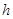 =1時,求跳水曲線所在的拋物線方程;
=1時,求跳水曲線所在的拋物線方程;
(2)若跳水運動員在區域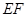 內入水時才能達到壓水花的訓練要求,求達到壓水花的訓練要求時
內入水時才能達到壓水花的訓練要求,求達到壓水花的訓練要求時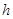 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com