
已知函數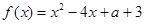 ,
,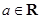 .
.
(Ⅰ)若函數 在
在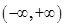 上至少有一個零點,求
上至少有一個零點,求 的取值范圍;
的取值范圍;
(Ⅱ)若函數 在
在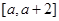 上的最大值為
上的最大值為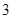 ,求
,求 的值.
的值.
(Ⅰ)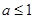 ;(Ⅱ)
;(Ⅱ)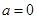 或
或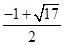 .
.
解析試題分析:(Ⅰ)根據方程的根與函數的零點的關系,將問題轉化為函數對應的方程有至少一個根,那么由判別式與根的個數的關系可知,只要判別式大于或等于0即可,列不等式求解;(Ⅱ)先求出二次函數的對稱軸,看看所給的閉區間與對稱軸的關系,分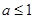 和
和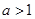 兩種情況進行討論:當
兩種情況進行討論:當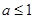 時,左半區間在對稱軸的左邊,最大值是
時,左半區間在對稱軸的左邊,最大值是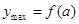 ;當
;當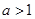 時,右半區間在對稱軸的右邊,最大值是
時,右半區間在對稱軸的右邊,最大值是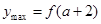 .然后結合最大值是3來求解.
.然后結合最大值是3來求解.
試題解析:(Ⅰ)依題意,函數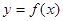 在
在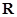 上至少有一個零點
上至少有一個零點
即方程 至少有一個實數根. 2分
至少有一個實數根. 2分
所以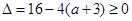 ,
,
解得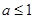 . 5分
. 5分
(Ⅱ)函數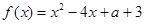 圖象的對稱軸方程是
圖象的對稱軸方程是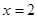 .
.
①當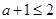 ,即
,即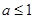 時,
時,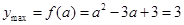 .
.
解得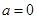 或
或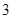 .又
.又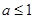 ,
,
所以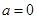 . 9分
. 9分
② 當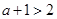 ,即
,即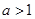 時,
時,
解得 .又
.又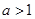 ,
,
所以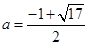 . 13分
. 13分
綜上,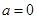 或
或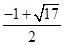 . 14分
. 14分
考點:1.方程的根與函數的零點的關系;2.二次函數的圖像與性質;3.二次函數在閉區間上的最值;4.解不等式


科目:高中數學 來源: 題型:解答題
島A觀察站發現在其東南方向有一艘可疑船只,正以每小時10海里的速度向東南方向航行,觀察站即刻通知在島A正南方向B處巡航的海監船前往檢查.接到通知后,海監船測得可疑船只在其北偏東75°方向且相距10海里的C處,隨即以每小時10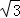 海里的速度前往攔截.
海里的速度前往攔截.
(I)問:海監船接到通知時,距離島A多少海里?
(II)假設海監船在D處恰好追上可疑船只,求它的航行方向及其航行的時間.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對于函數 若存在
若存在 ,使得
,使得 成立,則稱
成立,則稱 為
為 的不動點.
的不動點.
已知
(1)當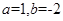 時,求函數
時,求函數 的不動點;
的不動點;
(2)若對任意實數 ,函數
,函數 恒有兩個相異的不動點,求
恒有兩個相異的不動點,求 的取值范圍;
的取值范圍;
(3)在(2)的條件下,若 圖象上
圖象上 、
、 兩點的橫坐標是函數
兩點的橫坐標是函數 的不動點,且
的不動點,且 、
、 兩點關于直線
兩點關于直線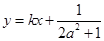 對稱,求
對稱,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
“城中觀海”是近年來國內很多大中型城市內澇所致的現象,究其原因,除天氣因素、城市規劃等原因外,城市垃圾雜物也是造成內澇的一個重要原因。暴雨會沖刷城市的垃圾雜物一起進入下水道,據統計,在不考慮其它因素的條件下,某段下水道的排水量V(單位:立方米/小時)是雜物垃圾密度x(單位:千克/立方米)的函數。當下水道的垃圾雜物密度達到2千克/立方米時,會造成堵塞,此時排水量為0;當垃圾雜物密度不超過0.2千克/立方米時,排水量是90立方米/小時;研究表明,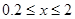 時,排水量V是垃圾雜物密度x的一次函數。
時,排水量V是垃圾雜物密度x的一次函數。
(Ⅰ)當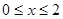 時,求函數V(x)的表達式;
時,求函數V(x)的表達式;
(Ⅱ)當垃圾雜物密度x為多大時,垃圾雜物量(單位時間內通過某段下水道的垃圾雜物量,單位:千克/小時) 可以達到最大,求出這個最大值。
可以達到最大,求出這個最大值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知一企業生產某產品的年固定成本為10萬元,每生產千件需另投入2.7萬元,設該企業年內共生產此種產品 千件,并且全部銷售完,每千件的銷售收入為
千件,并且全部銷售完,每千件的銷售收入為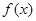 萬元,且
萬元,且
(1)寫出年利潤 (萬元)關于年產品
(萬元)關于年產品 (千件)的函數解析式;
(千件)的函數解析式;
(2)年產量為多少千件時,該企業生產此產品所獲年利潤最大?
(注:年利潤=年銷售收入-年總成本)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工廠有 名工人,現接受了生產
名工人,現接受了生產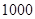 臺
臺 型高科技產品的總任務.已知每臺
型高科技產品的總任務.已知每臺 型產品由
型產品由 個
個 型裝置和
型裝置和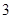 個
個 型裝置配套組成,每個工人每小時能加工
型裝置配套組成,每個工人每小時能加工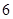 個
個 型裝置或
型裝置或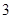 個
個 型裝置.現將工人分成兩組同時開始加工,每組分別加工一種裝置(完成自己的任務后不再支援另一組).設加工
型裝置.現將工人分成兩組同時開始加工,每組分別加工一種裝置(完成自己的任務后不再支援另一組).設加工 型裝置的工人有
型裝置的工人有 人,他們加工完
人,他們加工完 型裝置所需時間為
型裝置所需時間為 ,其余工人加工完
,其余工人加工完 型裝置所需時間為
型裝置所需時間為 (單位:小時,可不為整數).
(單位:小時,可不為整數).
(1)寫出 、
、 的解析式;
的解析式;
(2)寫出這 名工人完成總任務的時間
名工人完成總任務的時間 的解析式;
的解析式;
(3)應怎樣分組,才能使完成總任務用的時間最少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com