
某工廠有 名工人,現接受了生產
名工人,現接受了生產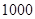 臺
臺 型高科技產品的總任務.已知每臺
型高科技產品的總任務.已知每臺 型產品由
型產品由 個
個 型裝置和
型裝置和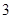 個
個 型裝置配套組成,每個工人每小時能加工
型裝置配套組成,每個工人每小時能加工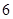 個
個 型裝置或
型裝置或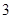 個
個 型裝置.現將工人分成兩組同時開始加工,每組分別加工一種裝置(完成自己的任務后不再支援另一組).設加工
型裝置.現將工人分成兩組同時開始加工,每組分別加工一種裝置(完成自己的任務后不再支援另一組).設加工 型裝置的工人有
型裝置的工人有 人,他們加工完
人,他們加工完 型裝置所需時間為
型裝置所需時間為 ,其余工人加工完
,其余工人加工完 型裝置所需時間為
型裝置所需時間為 (單位:小時,可不為整數).
(單位:小時,可不為整數).
(1)寫出 、
、 的解析式;
的解析式;
(2)寫出這 名工人完成總任務的時間
名工人完成總任務的時間 的解析式;
的解析式;
(3)應怎樣分組,才能使完成總任務用的時間最少?
(1) ,
, (
( ,
, );
);
(2) ;
;
(3)加工 型裝置,
型裝置, 型裝置的人數分別為
型裝置的人數分別為 、
、 或
或 、
、 .
.
解析試題分析:(1)根據定義求出函數 與
與 的解析式,并求出函數的定義域;(2)對兩個函數
的解析式,并求出函數的定義域;(2)對兩個函數 與
與 作差,比較
作差,比較 與
與 的大小,根據相應的
的大小,根據相應的 的取值范圍確定
的取值范圍確定 的解析式;(3)考查函數
的解析式;(3)考查函數 在每段定義域上的單調性,并求出函數
在每段定義域上的單調性,并求出函數 相應的最小值,從而確定加工兩種不同的零件的人數.
相應的最小值,從而確定加工兩種不同的零件的人數.
試題解析:(1)由題意知,需加工 型裝置4000個,加工
型裝置4000個,加工 型裝置3000個,所用工人分別為
型裝置3000個,所用工人分別為 人和(
人和( )
)
人,∴ ,
, ,
,
即 ,
, (
( ,
, ) 4分
) 4分
(2)

 ,
,
∵ ,∴
,∴ ,
,
當 時,
時, ,
, ,
, ,
,
當 時,
時, ,
, ,
, ,
, 9分
9分
(3)完成總任務所用時間最少即求 的最小值,
的最小值,
當 時,
時, 遞減,∴
遞減,∴
 ,
,
∴ ,此時
,此時 , 11分
, 11分
當 時,
時, 遞增,∴
遞增,∴
 ,
,
∴ ,此時
,此時 , 13分
, 13分
∴ ,
,
∴加工G型裝置,H型裝置的人數分別為86、130或87、129. 14分
考點:1.分段函數;2.分段函數的單調性與最值


 發散思維新課堂系列答案
發散思維新課堂系列答案科目:高中數學 來源: 題型:解答題
集合A是由適合以下性質的函數 構成的:對于定義域內任意兩個不相等的實數
構成的:對于定義域內任意兩個不相等的實數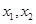 ,都有
,都有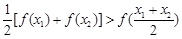 .
.
(1)試判斷 =
=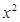 及
及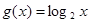 是否在集合A中,并說明理由;
是否在集合A中,并說明理由;
(2)設 ÎA且定義域為(0,+¥),值域為(0,1),
ÎA且定義域為(0,+¥),值域為(0,1), ,試寫出一個滿足以上條件的函數
,試寫出一個滿足以上條件的函數 的解析式,并給予證明.
的解析式,并給予證明.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
統計表明:某種型號的汽車在勻速行駛中每小時的耗油量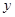 (升)關于行駛速度
(升)關于行駛速度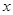 (千米/每小時)的函數解析式可以表示為
(千米/每小時)的函數解析式可以表示為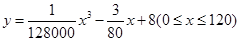 ,已知甲、乙兩地相距100千米.
,已知甲、乙兩地相距100千米.
(1)當汽車以40千米/小時的速度行駛時,從甲地到乙地要耗油多少升?
(2)當汽車以多大速度行駛時,從甲地到乙地耗油最少?最少為多少升?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數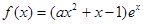 ,其中
,其中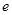 是自然對數的底數,
是自然對數的底數,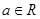 .
.
(1)若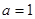 ,求曲線
,求曲線 在點
在點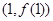 處的切線方程;
處的切線方程;
(2)若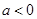 ,求
,求 的單調區間;
的單調區間;
(3)若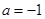 ,函數
,函數 的圖象與函數
的圖象與函數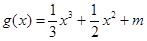 的圖象有3個不同的交點,求實數
的圖象有3個不同的交點,求實數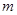 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某跳水運動員在一次跳水訓練時的跳水曲線為如圖所示的拋物線一段,已知跳水板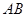 長為2m,跳水板距水面
長為2m,跳水板距水面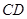 的高
的高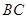 為3m,
為3m, =5m,
=5m,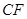 =6m,為安全和空中姿態優美,訓練時跳水曲線應在離起跳點
=6m,為安全和空中姿態優美,訓練時跳水曲線應在離起跳點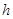 m(
m(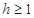 )時達到距水面最大高度4m,規定:以
)時達到距水面最大高度4m,規定:以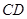 為橫軸,
為橫軸, 為縱軸建立直角坐標系.
為縱軸建立直角坐標系.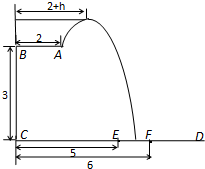
(1)當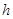 =1時,求跳水曲線所在的拋物線方程;
=1時,求跳水曲線所在的拋物線方程;
(2)若跳水運動員在區域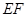 內入水時才能達到壓水花的訓練要求,求達到壓水花的訓練要求時
內入水時才能達到壓水花的訓練要求,求達到壓水花的訓練要求時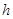 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com