
(本小題滿分14分)
已知函數(shù)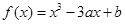 在
在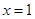 處有極小值
處有極小值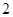 。
。
(1)求函數(shù)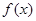 的解析式;
的解析式;
(2)若函數(shù)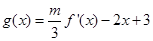 在
在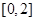 只有一個零點,求
只有一個零點,求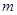 的取值范圍。
的取值范圍。
(1) (2)
(2) ,或
,或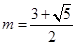 ,或
,或
解析試題分析:(1) 1分
1分
依題意有 , 3分
, 3分
解得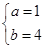 , 4分
, 4分
此時 ,
,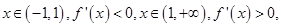 滿足
滿足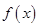 在
在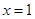 處取極小值
處取極小值
∴ 5分
5分
(2)
∴ …………6分
…………6分
當(dāng) 時,
時,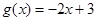 ,∴
,∴ 在
在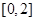 上有一個零點
上有一個零點 (符合),……8分
(符合),……8分
當(dāng) 時,
時,
①若方程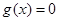 在
在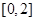 上有2個相等實根,即函數(shù)
上有2個相等實根,即函數(shù) 在
在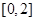 上有一個零點。
上有一個零點。
則 ,得
,得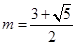 ……………………………………10分
……………………………………10分
②若 有2個零點,1個在
有2個零點,1個在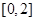 內(nèi),另1個在
內(nèi),另1個在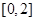 外,
外,
則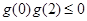 ,即
,即 ,解得
,解得 ,或
,或 …………12分
…………12分
經(jīng)檢驗 有2個零點,不滿足題意。
有2個零點,不滿足題意。
綜上: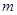 的取值范圍是
的取值范圍是 ,或
,或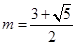 ,或
,或 ……………………14分
……………………14分
考點:本題考查了導(dǎo)數(shù)的運用
點評:導(dǎo)數(shù)本身是個解決問題的工具,是高考必考內(nèi)容之一,高考往往結(jié)合函數(shù)甚至是實際問題考查導(dǎo)數(shù)的應(yīng)用,求單調(diào)、最值、完成證明等,請注意歸納常規(guī)方法和常見注意點.


 名牌學(xué)校分層周周測系列答案
名牌學(xué)校分層周周測系列答案 黃岡海淀全程培優(yōu)測試卷系列答案
黃岡海淀全程培優(yōu)測試卷系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)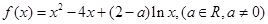
(I)當(dāng)a=18時,求函數(shù)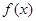 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(II)求函數(shù)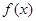 在區(qū)間
在區(qū)間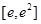 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)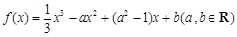
⑴若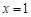 為
為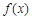 的極值點,求
的極值點,求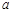 的值;
的值;
⑵若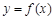 的圖象在點
的圖象在點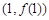 處的切線方程為
處的切線方程為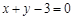 ,求
,求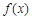 在區(qū)間
在區(qū)間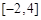 上的最大值;
上的最大值;
⑶當(dāng)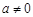 時,若
時,若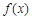 在區(qū)間
在區(qū)間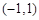 上不單調(diào),求
上不單調(diào),求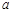 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分13分)
已知函數(shù)
(I)若曲線 在點
在點 處的切線與直線
處的切線與直線 垂直,求a的值;
垂直,求a的值;
(II)求函數(shù)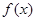 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com