
(08年泉州一中適應(yīng)性練習(xí)文)(12分)
如圖, PA⊥平面ABCD,ABCD為正方形, PA=AD=2,E、F、G分別是線段PA、PD、CD的中點.
(1)求證:PB∥面EFG;
(2)求異面直線EG與BD所成的角;
(3)求點A到平面EFG的距離。

解析:解法一:
(1)證明:取AB中點H,連結(jié)GH,HE,
∵E,F(xiàn),G分別是線段PA、PD、CD的中點,
∴GH∥AD∥EF,
∴E,F(xiàn),G,H四點共面. ……………………1分
又H為AB中點,
∴EH∥PB. ……………………………………2分
又EH![]() 面EFG,PB
面EFG,PB![]() 平面EFG,
平面EFG,
∴PB∥平面EFG. ………………………………4分
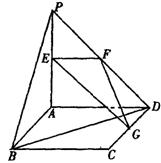
(2)解:取BC的中點M,連結(jié)GM、AM、EM,則GM//BD,
∴∠EGM(或其補角)就是異面直線EG與BD
所成的角.………………5分
在Rt△MAE中, ![]() ,
,
同理![]() ,…………………………6分
,…………………………6分
又![]() ,
,
∴在△MGE中,
![]() ………………7分
………………7分
故異面直線EG與BD所成的角為arccos![]() ,………………………………8分
,………………………………8分
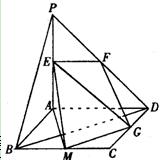
解法二:建立如圖所示的空間直角坐標系A(chǔ)-xyz,
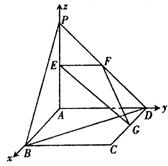
則A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),
P(0,0,2),E(0,0,1),F(xiàn)(0,1,1),G(1,2,0).
(1)證明:![]()
![]() …………………………1分
…………………………1分
設(shè)![]() ,
,
即![]() ,
,

![]() ……………3分
……………3分
![]() ,
,
∴PB∥平面EFG. …………………………………………………………………… 4分
(2)解:∵![]() ,…………………………………………5分
,…………………………………………5分
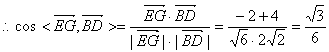 ,……………………… 7分
,……………………… 7分
故異面直線EG與BD所成的角為arccos![]() ,………………………………8分
,………………………………8分
(3) ![]()
![]() ,
,![]()
設(shè)面![]() 的法向量
的法向量![]()
則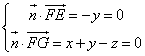
取法向量![]()
![]() A到平面EFG的距離
A到平面EFG的距離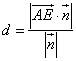 =
=![]() .…………………………12分
.…………………………12分


科目:高中數(shù)學(xué) 來源:湖南模擬 題型:單選題
| A.8 | B.32 | C.45 | D.72 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
| x1+x2 |
| 2 |
| x1x2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
| x |
| x2+2(a+2)x+3a |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com