
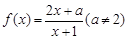 .
. 不可能為偶函數;
不可能為偶函數; 在
在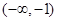 上單調遞減的充要條件是
上單調遞減的充要條件是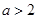 .
. 是偶函數,既然是偶函數,則對定義域內的一切x都有
是偶函數,既然是偶函數,則對定義域內的一切x都有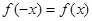 成立,那么我們為了說明假設不成立,即
成立,那么我們為了說明假設不成立,即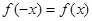 不可能成立,只需任取一個特殊值代入檢驗即可;(2)由于是證明函數
不可能成立,只需任取一個特殊值代入檢驗即可;(2)由于是證明函數 在
在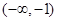 上單調遞減的充要條件是:
上單調遞減的充要條件是: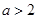 ;應分充分性和必要性兩個方面來加以證明,先證充分性:
;應分充分性和必要性兩個方面來加以證明,先證充分性: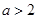 來證明
來證明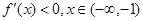 一定成立;再證必要性:由函數
一定成立;再證必要性:由函數 在
在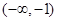 上單調遞減
上單調遞減
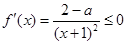 在
在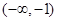 上恒成立,來證明
上恒成立,來證明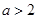 即可,注意已知中的
即可,注意已知中的 這一條件.
這一條件. 是偶函數, 2分
是偶函數, 2分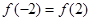 ,即
,即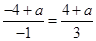 ,解得
,解得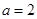 , 4分
, 4分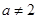 矛盾,所以函數
矛盾,所以函數 不可能是偶函數. 6分
不可能是偶函數. 6分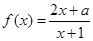 ,所以
,所以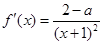 . 8分
. 8分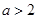 時,
時,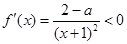 ,
, 在
在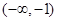 單調遞減; 10分
單調遞減; 10分 在
在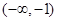 單調遞減時,
單調遞減時,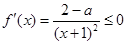 ,即
,即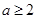 ,又
,又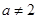 ,所以
,所以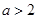 . 13分
. 13分

 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案 黃岡海淀全程培優測試卷系列答案
黃岡海淀全程培優測試卷系列答案科目:高中數學 來源:不詳 題型:解答題
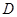 的函數
的函數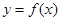 ,若同時滿足:
,若同時滿足: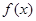 在
在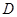 內單調遞增或單調遞減;
內單調遞增或單調遞減;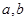 ]
]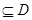 ,使
,使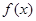 在
在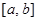 上的值域為
上的值域為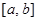 ;
;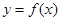 (
(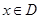 )叫做閉函數.
)叫做閉函數.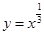 符合條件②的區間
符合條件②的區間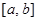 ;
;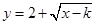 是閉函數,求實數
是閉函數,求實數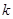 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| 1 |
| x2+1 |
|
| A.1個 | B.2個 | C.3個 | D.4個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com