
 。
。 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源:不詳 題型:單選題
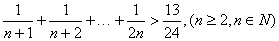 ”的過程中,
”的過程中,A.增加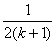 | B.增加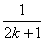 和 和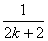 |
C.增加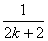 ,并減少 ,并減少 | D.增加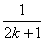 和 和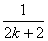 ,并減少 ,并減少 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
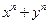 能被
能被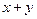 整除”,在第二步時,正確的證法是( )
整除”,在第二步時,正確的證法是( )A.假設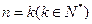 ,證明 ,證明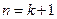 命題成立 命題成立 |
B.假設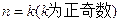 ,證明 ,證明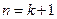 命題成立 命題成立 |
C.假設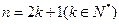 ,證明 ,證明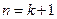 命題成立 命題成立 |
D.假設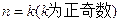 ,證明 ,證明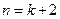 命題成立 命題成立 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com