若存在實數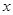
滿足不等式
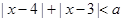，則實數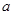
的取值范圍是( )
A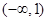． | B． |
C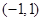． | D． |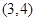
B
解析試題分析：解：設f（x）=|x-4|+|x-3|，當x＜3時，f（x）=-（x-4）-（x-3）=-2x+7，
故此時有f（x）=-2x+7＞1．，當x＞4，f（x）=（x-4）+（x-3）=2x-7，，故此時有f（x）=2x-7＞1．，當3≤x≤4，f（x）=-（x-4）+（x-3）=1，，綜上所述f（x）的最小值為1，，又因為原不等式|x-4|+|x-3|＜a有實數解，只要a大于f（x）的最小值即可．，所以a的取值范圍是（1，+∞）．故選B.
考點：絕對值不等式的解法
點評：此題主要考查絕對值不等式的解法，對于含有一個絕對值的不等式可以直接去絕對值號求解，對于含有兩個絕對值號的絕對值不等式需要用分類討論的方法去絕對值號．同學們需要注意選擇合適的解法
科目：高中數學 來源： 題型：單選題
若定義在R上的函數f(x)滿足
,且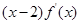
<0，a="f" (
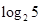),b="f" (
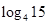),c="f" (
)，則a,b,c的大小關系為
| A．a>b>c | B．c>b>a | C．b>a>c | D．c>a>b |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，則不等式
的解集為 （ ）
和不等式
的解集相同，則
的值為（ ）
，
，對于任意
，不等式
恒成立，則實數
的取值范圍為（ ）
>0的解集為(-1，2)，
是
和
的等比中項，那么
=
的解集是
,
,則
滿足（ ）
