
 如圖,已知BC是半徑為1的半圓O的直徑,A是半圓周上不同于B,C的點,F為
如圖,已知BC是半徑為1的半圓O的直徑,A是半圓周上不同于B,C的點,F為 的中點.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求證:
的中點.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求證: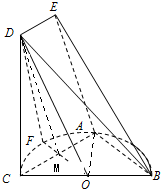 如圖,設OF∩AC=M,連接DM,OA
如圖,設OF∩AC=M,連接DM,OA 的中點
的中點 的中點,得M為AC的中點,所以DE∥
的中點,得M為AC的中點,所以DE∥ AC,得四邊形AMDE為平行四邊形,從而DM∥AE,DM∥平面ABE;由OM∥AB得,OM∥平面ABE;由兩個平面平行的判定定理,可知平面OFD∥平面BAE.
AC,得四邊形AMDE為平行四邊形,從而DM∥AE,DM∥平面ABE;由OM∥AB得,OM∥平面ABE;由兩個平面平行的判定定理,可知平面OFD∥平面BAE.

 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:高中數學 來源: 題型:
 (2012•藍山縣模擬)如圖,已知BC是半徑為1的半圓O的直徑,A是半圓周上不同于B,C的點,F為
(2012•藍山縣模擬)如圖,已知BC是半徑為1的半圓O的直徑,A是半圓周上不同于B,C的點,F為 | AC |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,已知BC是半徑為1的半圓O的直徑,A是半圓周上不同于B,C的點,又DC⊥面ABC,四邊形ACDE為梯形,DE∥AC,且AC=2DE,DC=2,二面角B-DE-C的大小為θ,tanθ=
如圖,已知BC是半徑為1的半圓O的直徑,A是半圓周上不同于B,C的點,又DC⊥面ABC,四邊形ACDE為梯形,DE∥AC,且AC=2DE,DC=2,二面角B-DE-C的大小為θ,tanθ=| 3 | 4 |
查看答案和解析>>
科目:高中數學 來源:2013年高考數學備考復習卷8:立體幾何(解析版) 題型:解答題
 的中點.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求證:
的中點.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求證:
查看答案和解析>>
科目:高中數學 來源:2012-2013學年湖南省永州市藍山二中等三校高三第四次聯考數學試卷(文科)(解析版) 題型:解答題
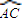 的中點.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求證:
的中點.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求證:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com