
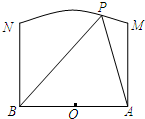
 如圖,兩個工廠A,B相距2km,點O為AB的中點,現要在以O為圓心,2km為半徑的圓弧MN上的某一點P處建一幢辦公樓,其中MA⊥AB,NB⊥AB.據測算此辦公樓受工廠A的“噪音影響度”與距離AP的平方成反比,比例系數是1,辦公樓受工廠B的“噪音影響度”與距離BP的平方也成反比,比例系數是4,辦公樓受A,B兩廠的“總噪音影響度”y是受A,B兩廠“噪音影響度”的和,設AP為xkm.
如圖,兩個工廠A,B相距2km,點O為AB的中點,現要在以O為圓心,2km為半徑的圓弧MN上的某一點P處建一幢辦公樓,其中MA⊥AB,NB⊥AB.據測算此辦公樓受工廠A的“噪音影響度”與距離AP的平方成反比,比例系數是1,辦公樓受工廠B的“噪音影響度”與距離BP的平方也成反比,比例系數是4,辦公樓受A,B兩廠的“總噪音影響度”y是受A,B兩廠“噪音影響度”的和,設AP為xkm.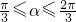 ;
;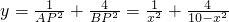 ;
;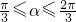 ,則
,則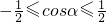 ,∴3≤5-4cosα≤7,
,∴3≤5-4cosα≤7, ;
;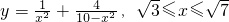 .
.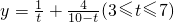 ;
; ;
; ,或t=-10(舍去),
,或t=-10(舍去),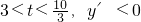 ,函數在
,函數在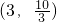 上單調遞減;
上單調遞減;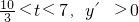 ,函數在
,函數在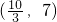 上單調遞增;
上單調遞增; 時,即
時,即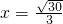 時,函數有最小值,
時,函數有最小值, km時,“總噪音影響度”最小.
km時,“總噪音影響度”最小.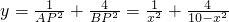 ;定義域由∠α的取值得出x的取值范圍即可.
;定義域由∠α的取值得出x的取值范圍即可.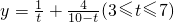 ;對y求導,令y'=0,得
;對y求導,令y'=0,得 時,函數有最小值,
時,函數有最小值, (km)時,“總噪音影響度”最小即可.
(km)時,“總噪音影響度”最小即可.

 挑戰100單元檢測試卷系列答案
挑戰100單元檢測試卷系列答案 名題金卷系列答案
名題金卷系列答案科目:高中數學 來源: 題型:
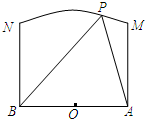 如圖,兩個工廠A,B相距2km,點O為AB的中點,現要在以O為圓心,2km為半徑的圓弧MN上的某一點P處建一幢辦公樓,其中MA⊥AB,NB⊥AB.據測算此辦公樓受工廠A的“噪音影響度”與距離AP的平方成反比,比例系數是1,辦公樓受工廠B的“噪音影響度”與距離BP的平方也成反比,比例系數是4,辦公樓受A,B兩廠的“總噪音影響度”y是受A,B兩廠“噪音影響度”的和,設AP為xkm.
如圖,兩個工廠A,B相距2km,點O為AB的中點,現要在以O為圓心,2km為半徑的圓弧MN上的某一點P處建一幢辦公樓,其中MA⊥AB,NB⊥AB.據測算此辦公樓受工廠A的“噪音影響度”與距離AP的平方成反比,比例系數是1,辦公樓受工廠B的“噪音影響度”與距離BP的平方也成反比,比例系數是4,辦公樓受A,B兩廠的“總噪音影響度”y是受A,B兩廠“噪音影響度”的和,設AP為xkm.查看答案和解析>>
科目:高中數學 來源: 題型:
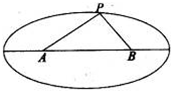 如圖,兩個工廠A,B(視為兩個點)相距2km,現要在以A,B為焦點,長軸長為4km的橢圓上某一點P處建一幢辦公樓.據測算此辦公樓受工廠A的“噪音影響度”與距離AP成反比,比例系數是1;辦公樓受工廠B的“噪音影響度”與距離BP也成反比,比例系數是4.辦公樓受A,B兩廠的“總噪音影響度”y是受A,B兩廠“噪音影響度”的和,設AP=xkm.
如圖,兩個工廠A,B(視為兩個點)相距2km,現要在以A,B為焦點,長軸長為4km的橢圓上某一點P處建一幢辦公樓.據測算此辦公樓受工廠A的“噪音影響度”與距離AP成反比,比例系數是1;辦公樓受工廠B的“噪音影響度”與距離BP也成反比,比例系數是4.辦公樓受A,B兩廠的“總噪音影響度”y是受A,B兩廠“噪音影響度”的和,設AP=xkm.查看答案和解析>>
科目:高中數學 來源: 題型:
如圖,兩個工廠A、B相距3(Km),現要在以AB為直徑的圓弧上的某一點![]() 處建一幢辦公樓(異于A、B點).據測算此辦公樓受工廠A的“噪音影響度”與距離AP的平方成反比,比例系數是1;辦公樓受工廠B的“噪音影響度” 與距離BP的平方也成反比,比例系數是4。辦公樓受A、B兩廠的“總噪音影響度”y是為受A、B兩廠“噪音影響度”之和,設AP為x(Km).
處建一幢辦公樓(異于A、B點).據測算此辦公樓受工廠A的“噪音影響度”與距離AP的平方成反比,比例系數是1;辦公樓受工廠B的“噪音影響度” 與距離BP的平方也成反比,比例系數是4。辦公樓受A、B兩廠的“總噪音影響度”y是為受A、B兩廠“噪音影響度”之和,設AP為x(Km).
 (1)求“總噪音影響度” y關于x的函數關系式,并指出函數的定義域;
(1)求“總噪音影響度” y關于x的函數關系式,并指出函數的定義域;
(2)當AP為多少時,“總噪音影響度”最小.
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,兩個工廠A,B相距2
如圖,兩個工廠A,B相距2 ![]() km,點O為AB的中點,現要在以O為圓心,2 km為半徑的圓弧MN上的某一點P處建一幢辦公樓,其中MA⊥AB,NB⊥AB.據測算此辦公樓受工廠A的“噪音影響度”與距離AP的平方成反比
km,點O為AB的中點,現要在以O為圓心,2 km為半徑的圓弧MN上的某一點P處建一幢辦公樓,其中MA⊥AB,NB⊥AB.據測算此辦公樓受工廠A的“噪音影響度”與距離AP的平方成反比![]() ,比例系數是1,辦公樓受工廠B
,比例系數是1,辦公樓受工廠B![]() 的“噪音影響度”與距離BP的平方也成反比,比例系數是4,辦公樓受A,B兩廠的“總噪音影響度”y是受A,B兩廠“噪音影響度”的和,設AP為x km.
的“噪音影響度”與距離BP的平方也成反比,比例系數是4,辦公樓受A,B兩廠的“總噪音影響度”y是受A,B兩廠“噪音影響度”的和,設AP為x km.
(1)求“![]() 總噪音影響度”y關于x的函數關系,并求出該函數的定義域;
總噪音影響度”y關于x的函數關系,并求出該函數的定義域;
(2)當AP為多少時,“總噪音影響度”最小?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com